UNIONES ATORNILLADAS

 

Medellín, octubre 2021

 

Conexiones atornilladas.

Durante muchos años, se utilizó el remache para las conexiones entre elementos metálicos. Cuando se profesionalizó la soldadura, los remaches decayeron notablemente y la soldadura se convirtió en el método, casi universal de conectores. No obstante, ambos requieren mano de obra muy calificada y demasiada supervisión. En los últimos años han resurgido las conexiones por medio de pernos, que, aunque pueden ser más costosos que los remaches y la soldadura, cuando se suma mano de obra más conectores, al final puede ser más barato e igual de seguro.

¿Qué tan resistente es una estructura metálica? Una estructura metálica es tan resistente, como lo son sus conectores.

Los tres sistemas: remaches, tornillos y soldadura dañan parcialmente el material, bien sea porque se les perfora o bien porque se les somete a muy altas temperaturas.

Tipos principales de tornillos estructurales.

Los principales tipos de tornillos estructurales son los comunes A307 y los de alta resistencia A325 y A409.

Los tornillos A307 ASTM A-307, tornillos A307 o como se dice en la industria, grado 2, son los tornillos de acero más comunes en la industria por sus características de acero y por tener un precio más bajo a todos los demás.

Estos tornillos varían en diámetro de 1/4 “a 1-1 / 2” y se fabrican de acero al carbono de baja resistencia.

Los tornillos A307 normalmente se consiguen con cabeza hexagonal, para facilidad en la instalación. Actualmente, hay una tendencia a utilizar tornillos de alta resistencia en cualquier estructura, aunque bastaría con los tornillos A307. Lo ideal es utilizar A307 en estructuras pequeñas y dejar los de alta resistencia para las obras monumentales o con esfuerzos demasiado grandes.

 

Tamaño de huecos hechos con taladro, para tornillos normales.

 

Diámetro de 12 a 14 mm                                        Se agrega 1mm

Diámetro de 16 a 24 mm                                        Se agrega 2 mm

Diámetro > 24 mm                                                  Se agrega 3 mm

 

Tipo de juntas realizadas con pernos.

Fig 1 Arreglos de uniones a cortante

En la siguiente figura definimos algunos términos técnicos de las juntas hechas con tornillos.

Fig 2 Espaciamiento de tornillos con agujeros estándar.

Resistencia de diseño de sujetadores en ksi y kg/cm2

 

Descripción de los sujetadores	Resistencia a tensión		Resistencia a cortante en conexiones tipo aplastamiento
	Factor de resistencia Φ	Resistencia nominal en kg/cm2	Factor de resistencia Φ	Resistencia nominal  en kg/cm2
Tornillos A307 (Roscas no están excluidas de planos de corte.	0,75	45 ksi = 3169 kg/cm2	0,75	24ksi = 1690 kg/cm2
Tornillos A325 (Roscas no están excluidas de planos de corte.		90 ksi=6338 kg/cm2		48 ksi=3380 kg/cm2
Tornillos A490 (Roscas no están excluidas de planos de corte.		113 ksi = 7957 kg/cm2		60 ksi = 4225 kg/cm2

 

Fig. 3 resistencia de los tornillos estándar.

Para este blog, las deformaciones de las placas sujetadas por los pernos son importantes e igualmente el aplastamiento que los tornillos ejercen sobre estas platinas o elementos también y por razones de seguridad, se utilizará siempre el valor de 2,4dtFu, como máxima resistencia que resiste la placa a aplastamiento (aunque no haya falla visible), donde Fu es la resistencia última de la platina o elemento, d = ancho de la platina y t = la profundidad de la misma.

La experiencia muestra que estas platinas o elementos casi nunca fallan por aplastamiento, pero que los esfuerzos grandes de aplastamiento, si afectan el funcionamiento general de las platinas o elementos.

Ejemplo 1.

Calcular la fuerza Pu, que haga que la conexión mostrada en la figura, sea segura.

Platina de ½ pulg           fy=50 Ksi                                      Fu = 65Ksi

Tornillo 7/8 pulg, agujeros estándar (No se sabe si los planos de corte están dentro de la rosca.    Fv= 48 Ksi  (resistencia última)

Distancia al borde > 1 ½ d = (3/2) (7/8) = 1,31 pulg

Distancia centro a centro entre tornillos > 3d = 2,63 pulg

Figura 4 Ejemplo 1

¿Qué pasa con la platina?

Ag = 12x1/2 = 6 pulg2     (área gruesa = área total)

La platina queda sometida a una tensión de 0,75xfyAg = 0,75x50x6 = 225 Klb

En la parte de los huecos el área se reduce

An = 6 pulg2 – 2x (1/2) (7/8) = 5,1 pulg2,             Aefectiva = sección crítica

Aquí utilizamos Fu y no fy

La tensión que recibe en esta zona es 0,75x65x5,1 = 248 klb

¿Qué pasa con los tornillos?

 Cortante simple:           Pu = 0,75x0,6x48x4 = 86,4 klb

Aplastamiento              Pu= 0,75x2,4Fudt = 0,75x2,4x65x(7/8) (1/2)x4 = 204,7 klb

Este valor debe ser mayor que el encontrado de resistencia de los tornillos por cortante. Si La cortante simple fuese mayor , la conexión fallaría por aplastamiento de la platina.

El máximo Pu que resiste esta unión es 86400 lb = 39272 kg = 39 ton

Ejemplo 2

En la gráfica se ve una unión a cortante doble. El acero de las platinas es A36 (fy= 2500 kg/cm2 y Fu= 4000 kg/cm2). Se utilizan tornillos de 2 cm de diámetro (a tensión ft= 6338 kg/cm2 y a cortante y aplastamiento fv = 3380 kg/cm2). Área de un tornillo = 3,14 cm2.

Fig 5 Ejemplo 2

Solución:

Resistencia de diseño por cortante, por tornillo:

0,75x (2x3,14 cm2)3380 kg/cm2 = 15920 kg

Resistencia de diseño por aplastamiento, por tornillo:

0,75x2,4xFuxdxt         Fu del material de la platina, d diámetro tornillo, t espesor platina.

0,75x2,4x2 cmx2 cmx4000 kg/cm2 = 28800 kg Este valor debe ser mayor que el encontrado de resistencia del tornillo por cortante. Si este último valor fuese mayor a 28800, la conexión fallaría por aplastamiento de la platina.

Se requieren 136000 kg/ 15920 kg =8,5 tornillos,   = 9 tornillos

 Ejemplo 3

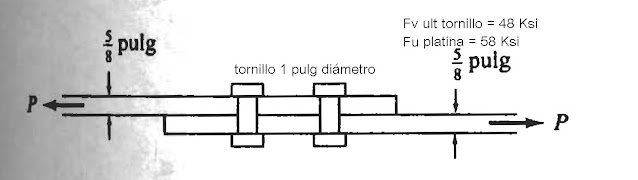
La conexión de la figura está sometido a una carga muerta Pd= 30 klb u una viva Pl = 50 klb El conector cumple las distancias entre tornillos y de tornillo a borde. El Fu de las platinas es 58 Ksi. Los tornillos son A325  y no se sabe si las áreas de corte caen en la región de las roscas, por tanto, utilizamos Fv ult = 48 Ksi

Fig 6 ejemplo 3

La carga mayorada será 1,2 PD + 1,6 PL = 116 Klb

Resistencia de un tornillo a fricción es: 0,75x 0,785 cm2 x 48 Ksi = 28,26 klb

(Área de cada tornillo de 1 pulg = 0,785 )

Resistencia del tornillo por aplastamiento

0,75x2,4x1 pulgx (5/8 pulg) x58 Ksi= 65,25 klb                   28,26<65,25 luego no hay falla por aplastamiento.

Número de tornillos 116 klb/28,26 klb              5 tornillos

Ejemplo 4

De van unir dos perfiles HEB300 e IPE300, el IPE está cargado con una carga mayorada de 2000 kg/m. El IPE tiene una luz de 6 m. Vamos a utilizar un ángulo 80x8 como platina que una los dos perfiles y en ese ángulo vamos a colocar 4 pernos, como se indica en la figura.

HEB300 altura h=300 mm, s (espesor del alma = 11 mm, ancho del flange (ala) b = 300 mm, t espesor del flange t = 19mm, Grado 50 fy =3500 kg/cm2, Fu = 4500 kg/cm2, Ix =25170 cm4, e Iy = 8563 cm4

IPE300 altura h=300 mm, s (espesor del alma = 7,1 mm, ancho del flange (ala) b = 115 mm, t espesor del flange t = 10,70 mm, Grado 50 fy =3500 kg/cm2, Fu = 4500 kg/cm2, Ix = 8356 cm4   Iy = 604 cm4

L 80x8   Grado 50.

Calcular el diámetro de los tornillos que se emplean en esta conexión. Vamos a utilizar tornillos comunes A307, Fv (ultima a cortante) = 1690 kg/cm2)

Fig 7 Ejemplo unión a momento entre un HEB y un IPE que trasmite momento.

En principio hay cuatro tornillos perforando el ala del HEB, cada uno con una superficie de falla y 2 sobre el alma del IPE, cada tornillo con dos superficies de falla por cortante. Esto puede cambiar.

Bajo la primera hipótesis, la viga se comporta como empotrada - empotrada, tiene 6 m de luz. Así en la unión del HEB300 y el IPE·300, la Vu = 2000 kg/mx 3m = 6000 kg y el momento Mu= ql²/12 = 6000 kg m

Cada tornillo que perfora el ala del HBE está sometido a una cortante de 1500 kg y cada uno de los que perforan el alma del IPE queda sometido a 3000 kg de cortante (1500 por superficie de falla). En el IPE. la cortante de 1500 kg = 0,75x1690 kg/cm2 x A, siendo A el área del tornillo en cm2.

A = 1,18 cm2 = 118 mm2           un tornillo de 16 mm tiene un Área = 2 cm2. Utilizaremos 2 tornillos de 16 mm de diámetro. (Nos excedemos un poco porque aparecerán cizalladuras y momentos adicionales)

Estimemos el aplastamiento:

la resistencia de la placa por un tornillo de 16 mm A307, en el IPE es: 0,75x2,4x 0,71x 1,6x 4500 = 9201 kg

Y el aplastamiento de cada tornillo contra la lámina del perfil es: 3000/2 = 1500 (En cada superficie de falla. kg)      9201 kg>1500 kg, o sea que por aplastamiento, no nos preocupamos.

Sigue vigente los 2 tornillos de 16 mm A307.

Arreglo geométrico de los tornillos.

e1 y e2 distancia del centro de los tornillos al borde de la platina > 1,5do, do el área del hueco para el tornillo = 18 mm         1,5x18 = 27 mm

distancia entre centros de tornillos >3do                54 mm

Escogemos la configuración mostrada en la fig (unión HEB e IPE)

Geometría de los tornillos en el ángulo 80x0

Hay dos ángulos, uno a cada lado del alma del IPE.

Nota. En realidad, el hecho de que la cortante no pasa por el eje de los tornillos, produce una flexión adicional, que es relativamente grande.

M1=6000 kgx0,05m = 300 kg m. Y este momento se puede reemplazar por un par de 300 kg m/0,095 m = 3157 kg

Si Este par H, aumenta la cizalladura normal en √ (6000 ² + (2x3157) ²) = 8800 kg y por tornillo será 4400 kg  (dividido en 2 superficies de falla)

La resistencia de un tornillo (por superficie de falla) será 0,75x3380 kg/cm2x 2cm2 = 5070 kg, o sea que los dos tornillos de 16 mm, resisten la cizalladura real aumentada de 4400/2 kg, en cada superficie de falla.

Fig. 8 momento y cizalladura creadas

Veamos si la disposición que hemos usado, con ángulo 80x8, tornillos 16 mm cumple con el momento.

M= 6000 kg m, se reemplaza por un par 6000/0,095 = 63158 kg, cada tornillo superior absorbería 31579 kg

La resistencia a tensión de un tornillo de 16 mm es 0,75x3169 kg/cm2 x 2 cm2 = 4753. Por tanto, se necesitarían 31579/4753 = 7 tornillos de 16 mm.

La solución, con la que habíamos trabajado no funciona y hay que cambiarla.. Hay 3 posibles nuevas soluciones a este problema: o cambiamos el ángulo o cambiamos los tornillos o cambiamos ángulo y tornillos.

Vamos a escoger esta última solución.

Por tanteo, buscamos un ángulo más grande y, además, cambiamos los tornillos por A325 y un diámetro de 20 cm. Ya no nos preocupamos por cizalladura, porque un tornillo inferior la resistía plenamente.

Después de varios tanteos, se ha seleccionado un ángulo 128x10 y vamos a colocar, ya no 1 sino 2 tornillos A325 por fila, separadas 12 cm.

La nueva placa conectora será así:

Fig 9 Nueva placa conectora

En los ángulos sobre el ala del HEB habrá cuatro tornillos superiores y 4 inferiores, separados 12 cm.

Para el nuevo tornillo d= 20

e1 y e2 >= 1,5x20 = 30 mm

p Distancia entre tornillos >=3d = 60 mm

La nueva distribución cumple esto.

El momento es 6000 kg m, que cambiamos por el par H = 6000/0.12 =50000 kg

Distribuimos estos 50000 entre 4 tornillos superiores en HEB que soportarán la tensión del momento. C/u = 50000/4 =12500 kg

La resistencia de cada tornillo a tensión será 0,75x6338x3.1 = 14736 kg. Por tanto, estos tornillos resisten la tracción, mientras los inferiores resisten la compresión y el momento se trasmite correctamente.

Para el caso de la platina que se pega al IPE, los tornillos reciben el mismo par, en 4 superficies de falla.

Cada uno resiste a cortante: 0.75x3380x3,1 =7858 kg < 12500 kg.

Lo cual indica que este tornillo no sirve tampoco. Requerimos un diámetro superior.

D= 24 mm      A = 4,5 cm2 = 450 mm2

e1 y e2 = 36 mm

p = 72 cm

Hay que aumentar el tamaño del ángulo por 152x10

Fig 10 Distribución final del conector, ángulo 152x10 y tornillos A325, d= 24 mm

Para el caso de la nueva platina 152x10, los tornillos d= 24 y A325, fv cortante última = 3380 kg/cm2 reciben el mismo par, en 4 superficies de falla, sobre la IPE.

Cada uno resiste a cortante: 0.75x3380x4,5=11407 kg

Como aumentamos la distancia entre las fuerzas del par la nueva fuerza será:40000 kg

10000 kg por cada superficie a cortante:

11407kg > 10000 kg

Y esta disposición si garantiza el empotramiento seguro.

La solución definitiva será.

2 ángulos 152x10, uno a cada lado del alma del IPE. Una longitud de ángulo de 222 mm,

8 tornillos d= 24 mm, en la disposición que se indica en la figura, incluyendo los que perforan el ala de HEB300. (4 tornillos en la IPE y 4 en la HEB)

No hay necesidad de más chequeos, ya que los tornillos de 16 mm resistían la cortante, los de 20 mm resistían el momento en el HEB300 y sólo los de 24 mm resistían el momento en el alma del IPE300. Si colocamos tornillos A325 de 24 mm en general, vamos por el lado de la seguridad. Y resisten todas las solicitaciones.

 

Juan Fernando Sanín Echeverri

juanfernando.sanin@gmail.com

 

Arco capaz - Construir un triángulo ABC, del cual se conoce: ángulo A y medianas que parten de B y C

 

Jardín, septiembre de 2021

 

Concepto de Arco Capaz

 

1.    “El arco capaz es el lugar geométrico de los puntos del plano, que unidos con los extremos de un segmento AB forman siempre, desde cada uno de esos puntos, un mismo ángulo.”

Fig 1 - 1

Se conoce el ángulo A (rojo) y la cuerda BC (azul).

·         Se colocan en un mismo plano el ángulo <A y la cuerda BC,          No importa su posición relativa.

·         Por B se traza una paralela a uno de los lados del ángulo conocido y por C se traza otra paralela al otro lado del ángulo. En la figura 1 estas paralelas (verde) se cortan en A y con toda seguridad el ángulo BAC = <A (por lados paralelos)

·         Hacemos pasar una circunferencia por los puntos A, B y C. Por M, punto medio de BC trazamos la mediatriz. Por N, punto medio de AC, trazamos la mediatriz. Estas mediatrices se cortan en el punto O, que equidista de los puntos ABC. Trazamos la circunferencia circunscrita. Cualquier ángulo cuyo vértice esté en el arco <DEA, subtendido por la cuerda BC, tiene como medida la mitad el arco de esa circunferencia  (en radianes)o, debajo de la curda BC, que en la figura Fig 1 – 1, se ha borrado.

 

1.   2. Construir un triángulo ABC, del cual se conoce: El ángulo interno A y las medianas que parten de B y C

Fig2 -1

Suponemos el problema resuelto.

Miremos la figura 2 – 2 (es la misma fig 2 – 1), con algunas líneas auxiliares.

Fig 2 - 2

El triángulo a construir es el triángulo ABC. Llamamos BM2 = m2, mediana trazada desde B. Llamamos CM3 = m3, la mediana trazada desde C.

Sabemos que las medianas se cortan a 2/3 del vértice y a 1/3 de la base. En la figura 2 -2, hemos hecho hincapié en esta propiedad. Las medianas se cortan en el punto G.

Lo primero que observamos es que es posible construir el arco capaz del ángulo A (conocido) y la cuerda BM2 (conocida). Se hace con el procedimiento indicado en el punto 1 del blog. Nótese que no se ha determinado el punto A.

Prolongamos la mediana BM2, una longitud (1/3)m2 y llegamos al punto D.

Ahora observamos que la figura ADCG es un paralelogramo, (ya que es un cuadrilátero, cuyas diagonales se cortan en su punto medio. M2 es el punto medio de AC e igualmente el punto medio de GD.)

La distancia DA = (2/3)m3.

La construcción del triángulo ya está completada, porque tenemos el punto D y trazamos, desde D, una circunferencia cuyo radio sea (2/3)m3 y donde esta nueva circunferencia, corte el arco capaz de <A y BC, estará ubicado el punto A.

Sigue prolongar la línea AM2 una distancia igual y estaremos sobre el punto C.

El procedimiento es el siguiente:

Se construye la mediana m2 = BM2 (que es un dato del problema)

Se construye el arco capaz de BM2 y el ángulo <A conocido.

Se prolonga la mediana BM2 una distancia igual a (1/3)m2 y obtenemos el punto D.

Por D trazamos una circunferencia de radio igual a (2/3)m3, que cortará, en el punto A, el arco capaz que hemos construido.

Prolongamos la línea AM2 una distancia igual y llegamos al punto C.

El triángulo pedido se ha construido.

 

Juan Fernando Sanín E

juanfernando.sanin@gmail.com

 

Cuatro problemas de geometría Euclidiana Plana

 

Jardín, septiembre 2021

 

 

Cuatro problemas de geometría

 

1.    Construcción de una circunferencia.

Se sabe que los puntos A, B y D están sobre una circunferencia. Lo único que le entregan a uno es la parte del dibujo que está en rojo. Hallar el radio de esa circunferencia.

Fig 1 -1

Cuando me presentaron el problema, se me ocurrió una solución obvia. La de la figura B. Se escoge un sistema de coordenadas y se conocen 3 puntos de la misma. La ecuación de esa circunferencia es       (x – h)² + (y – k)² = R²          donde (h, k) es el centro de la misma y R el radio.

A (0,0)

h² + k² = R²                                                                                 (1)

B (0,4)

h² + (4 – k)² = R²                                                                        (2)

C (6, 6)

(6 – h)² + (6 -k)² = R²                                                                     (3)

 Desarrollemos la (2)          h² + 16 - 8k + k² = R²                         k =2

Desarrollemos la (3)         36 – 12h + h² + 36 – 12k + k² = R²

72 – 12h – 12k = 0                                                                        h =4

R = √ (2² + 4²) = 2√5

El problema, es que lo presentaron para resolverlo por geometría Euclidiana y haber encontrado primero la solución por geometría analítica, lo que me quitó espacio para maniobrar, ya que cualquier solución que encontraba, trataba de que fuera similar a esta solución.

Por geometría Euclidiana.

Fig 1 - 2

Trazamos la recta auxiliar AH, paralela a BC. Construimos la línea auxiliar DG.

Trazamos la recta auxiliar AH, paralela a BC. Construimos la línea auxiliar DG.

Si trazamos la línea MJ, paralela a BE y AH; (M punto medio de AB); Observando la figura, vemos que la línea MJ es parte de un diámetro. Concluimos que FG = 2.

 

Recordemos la propiedad de las rectas secantes de una circunferencia:

BCxCE = GCxCD

6xCE = 6x2

Por lo que CE = 2

La recta AE es el diámetro de la circunferencia, debido al ángulo recto en B.

(2R)² = 4² + 8²

 2R = √80 = 4√5                                          y    R = 2√5

2.  Encontrar el área en verde, en el triángulo ABC

Fig 2 - 1

Cualquiera sea el triángulo, conocidos los tres lados, siempre es posible encontrar el área, bien sea utilizando la ley del coseno, que nos permite encontrar un ángulo y una altura respecto de uno de los lados o por el método de Herón

A= √ (s (s – a) (s – b) (s – c))                                      s= (a + b + c)/2

No obstante, podemos sospechar que se trata de un triángulo rectángulo.

√ (28² + 21²) = √1225 = 35

Recordemos la propiedad, de que las tangentes trazadas a una circunferencia, son iguales.

Planteamos 3 ecuaciones con 3 incógnitas x, y, r

x + 2r + y = 35                                                                        (1)

Veamos la figura de otra manera:

Fig 2 - 2

Recordemos las fórmulas de trigonometría

cos A/2 = √ ((1 + cosA) /2)

sen A/2 = √ ((1 - cosA) /2)

En la figura 2 – 2                       cos A/2 = √ ((1 + 28/35) /2) = x/√ (x² + r²)

√ (63/70) = x/√ (x² + r²)            x = (3/√10) √ (x² + r²)                                      (2)

cos B/2 = √ ((1 + 21/35) /2) = y/√ (y² + r²)            y = (2/√5) √ (y² + r²)              (3)

La (2) la convertimos en 10x² = 9x² + 9r²                x² = 9r²         x = 3r

La (3) la convertimos en 5y² = 4y² + 4r²                   y² = 4r²        y = 2r

x + y = 5r

La (1) se convierte en 5r + 2r = 35                               r = 5

El área verde es igual a 21x28/2 - 2p (25) = 294 – 157,08 = 136,92 m2

3. Encontrar el área que está sombreada en rojo.

Fig 3 - 1

El área solicitada es igual a la mitad del rectángulo – área sector B - área sector D

Veamos la figura Fig 3 -2

Fig 3 -2

En la figura 3 – 2 está claro que el área solicitada es igual al área del triángulo rectángulo inferior – área del círculo de radio 1

= 4 – p (1)² = 0,858 unidades de área

 

1.   4.  Construir un triángulo del cual se conocen.

La altura, la bisectriz y la mediana que parten de un mismo vértice.

Fig 4 - 1

Altura, bisectriz y mediana, trazadas desde un mismo vértice.

Suponemos el problema resuelto.

Las tres líneas que conocemos tienen el pie, sobre el lado a, que no conocemos.

Construcción:

Trazamos una línea horizontal. (De esta recta va a salir la base a)

Trazamos una perpendicular a la línea anterior, con una longitud igual a la altura. Aquí obtenemos el vértice A y el pie H de la altura.

Con centro en A y longitudes iguales a la bisectriz y a la mediana, ubicamos los puntos I y M

(I pie de la bisectriz y M pie de la mediana.)

Si miramos la figura 4 – 2, la prolongación de la bisectriz corta la mediatriz trazada desde M en un punto P. (La mediatriz referida es la perpendicular a la recta que contiene el lado a, en el punto M).

Si volvemos a mirar la figura 4 – 2, también conocemos la cuerda AP y el centro del círculo circunscrito se encuentra donde se cortan dos mediatrices. Trazamos una perpendicular a AP por su punto medio N y esta se intercepta con la primera mediatriz que trazamos por M.

Fig 4 - 2

En este momento tenemos el vértice A y el punto O, centro de la circunferencia circunscrita. Simplemente trazamos esta circunferencia y así obtenemos los puntos B y C.

 Atentamente,

 

 Juan Fernando Sanín E

juanfernando.sanin@gmail.com