Medellín Febrero 2011
Polinomio Característico, Valores propios, Vectores propios de una matriz cuadrada
Para facilitar la comprensión del tema, lo vamos a hacer con una matriz cuadrada 3x3, pero los resultados los podemos aplicar a cualquier clase de matriz cuadrada.
Polinomio característico de una matriz cuadrada. En este caso 3x3

4t3 - 5t2 + t=0 …………Este es el polinomio característico de la matriz A, en el cual t=0 es una de las raíces. Las otras dos raíces las encontramos solucionando la ecuación de segundo grado:
4t2 - 5t + 1=0
t=1 y t = ¼
Las raíces del polinomio característico son 1, 0, ¼
Estas raíces se denominan los valores propios de A. En una ecuación cúbica las raíces pueden ser: a) tres raíces reales (como es el caso) o b) una real y dos complejas y en este último caso la matriz A sólo tendría un valor propio real.
Estos valores propios tienen la siguiente propiedad:
Si v es un vector en R3, entonces
Av = tv
O lo que es lo mismo
Av – tIv = 0 ……………………..donde I es la matriz identidad 3x3
(A – tI)v = 0
Siendo v un vector diferente de 0, y M=A – tI = 0, entonces Mv=0, (v= (x1, x2 ,...xn) Traspuesto) es sistema de n ecuaciones lineales con n incognitas. Si det M fuese diferente de 0, entonces la única solución al sistema sería la solución trivial X=0 y como v es diferente de 0 la única opción razonable es que determinante M = 0.
O sea que det(A – tI) = 0, que es lo que llamamos anteriormente polinomio característico.
Para cada valor propio real de A, es posible encontrar al menos un vector columna 3x1. Ese vector lo llamaremos vector propio de A. (Eigenvalues y Eigenvectors)

Producto que nos da origen al siguiente conjunto de ecuaciones:
x-y =0
x-3y+2z=0
x+y-2z=0
Como el sistema tiene infinitas soluciones, de la primera escogemos arbitrariamente, por ejemplo x=5. Esto implica que y=5
De la tercera vemos que z=5
Si llevamos estos valores arbitrarios a la segunda obtenemos 5 -3x5+2x5 =0, o sea que el vector v1= (5, 5, 5)T es el primer vector propio v1, correspondiente al valor propio t=1.
Con un razonamiento similar encontramos el v2 correspondiente a t=0
MX=0
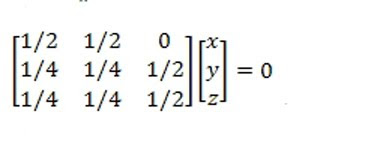
x+y=0
x+y+2z=0
Si escogemos x=1 entonces y= -1 y z=0 por lo que el vector propio v2, correspondiente al valor propio t=0 es v2 = (1, -1, 0)T.
Y v3 correspondiente al valor t = ¼ será
MX=0
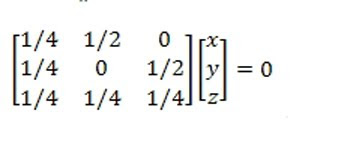
x+2y=0
x+2z=0
x+y+z=0
De la primera tomamos x= 2 lo que nos entrega y= -1
De la segunda encontramos que z= -1
Este vector satisface la tercera ecuación
V3=(2, -1, -1) T
Definimos una matriz P formada por los vectores v1, v2 y v3 en el orden en que definimos los valores característicos t1, t2 y t3
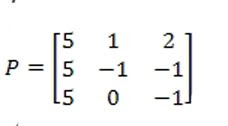
Verificamos que P tenga inversa:
Det P=15 Por lo tanto existe P -1
Por cualquiera de los métodos encontramos la inversa de P.

El resultado es una matriz diagonal D, cuya diagonal son los números 1, 0, ¼ que eran los valores propios de la matriz A. Por tanto, si existen P y P-1 entonces:
P-1AP=D
Premultiplicando por P y postmultiplicando por P-1 obtenemos:
A=PDP-1…………….. (1)
Si la matriz A3x3 tiene 3 valores propios reales, entonces la matriz se puede factorizar como se indica en la fórmula (1).
Otra propiedad importante de esta factorización es la siguiente:
An=PDnP-1
Donde Dn es la matriz diagonal, en la cual los valores de la diagonal de D se han elevado al exponente n. Las matrices P y P-1 se conservan igual.
Para este caso
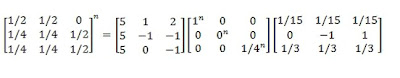
Qué pasaría si n=-1?
Obtendríamos la inversa de A. En este caso, esto no es posible, ya que el detA=0 y por tanto A no tiene inversa. Si hubiéramos escogido una matriz A, no singular para el ejemplo, haciendo n=1 obtendríamos la matriz A -1.
Juan Fernando Sanin
Juanfernando.sanin@gmail.com