Medellín diciembre 2023
Sistemas de numeración
Cuando trabajamos las operaciones aritméticas, se hará en
sistema decimal. Sin embargo, existen otros sistemas de numeración, y algunos
forman parte también de las actividades cotidianas. Así, el sistema binario es
básico en el funcionamiento de los ordenadores, y el sexagesimal se utiliza
para medir los valores de los ángulos y el cómputo del tiempo de los relojes,
entre otras tareas.
Un sistema de numeración puede definirse como un conjunto de signos, relaciones, convenios y normas destinados a expresar de modo gráfico y verbal el valor de los números y las cantidades numéricas.
·
La base del
sistema, que se define como un convenio de agrupación de sus unidades. Por
ejemplo, la base 10 o decimal agrupa diez unidades, mientras que, la binaria
únicamente agrupa dos.
·
Los numerales
del sistema, o cifras elementales que se utilizan, según la base. En el sistema
decimal, se usan los numerales 0, 1, 2, 3, 4, 5, 6, 7, 8 y 9. En cambio, en el
sistema binario tan sólo se emplean el 0 y el 1.
En base 2, sólo hay dos dígitos: 0 y
1
Escribiremos en base 2 algunos
números, que vamos a indicar en base 10
|
Base 10 |
Base 2 |
|
1 |
01 |
|
2 |
10 |
|
3 |
11 |
|
4 |
100 |
|
5 |
101 |
|
6 |
110 |
|
100 |
1100100 |
|
Base 10 |
Base 3 |
|
1 |
01 |
|
2 |
10 |
|
3 |
11 |
|
4 |
100 |
|
5 |
101 |
|
6 |
110 |
|
100 |
10201 |
La base 16, Hexadecimal tendrá16
dígitos: 0, 1, 2, 3, 4, 5, 6, 7, 7, 8, 9, A, B, C, D, E, F
A = 10, B = 11, C = 12, D = 13, E =
14 y F = 15
|
Decimal |
binario |
Ternario (b = 3) |
Octal (b= 8) |
Hexagecimal b =
16 |
|
0 |
0000 |
000 |
00 |
0 |
|
1 |
0001 |
001 |
01 |
1 |
|
2 |
0010 |
002 |
02 |
2 |
|
3 |
0011 |
010 |
03 |
3 |
|
4 |
0100 |
011 |
04 |
4 |
|
5 |
0101 |
012 |
05 |
5 |
|
6 |
0110 |
020 |
06 |
6 |
|
7 |
0111 |
021 |
07 |
7 |
|
8 |
1000 |
022 |
10 |
8 |
|
9 |
1001 |
100 |
11 |
9 |
|
10 |
1010 |
101 |
12 |
A |
|
11 |
1011 |
102 |
13 |
B |
|
12 |
1100 |
110 |
14 |
C |
|
13 |
1101 |
111 |
15 |
D |
|
14 |
1110 |
112120 |
16 |
E |
|
15 |
1111 |
|
17 |
F |
En este link, se pueden convertir,
online, números entre diferentes bases:
https://www.convertworld.com/es/sistemas-de-numeracion/
1254510 a base 8 = 304018
13245 a base 8 = 3268
1010101010102 = 273010
La base10 no se suele escribir.
Algoritmos de conversión entre
diferentes bases
Cualquier número en base 10, se puede
escribir en forma de potencias de 10.
Ej 2365 = 2x103+3x102+6x101+5x100
= 2000+300+60+65 =2365
Un número en base octal, de igual
manera, se puede escribir por medio de potencias de 8
34268 = 3x83+4x82+6x8+6 (1) recordar que en este caso 10 = 8
Si supiéramos hacer estas
operaciones, exponente, producto y suma en base 8, el resultado de la operación
sería 34268
Lo interesante es que, si hacemos
estas operaciones en base 10, obtenemos el número en base 10.
(Realmente no pude encontrar en la
WEB un soporte serio que justifique este resultado, pero es universal en todos
los libros de aritmética que consulté y aun en tesis de doctorado, e igual, dan
el algoritmo, por cierto, sin prueba.)
Haciendo la operación de la expresión
(1) en base 10 obtenemos:
3x512+4x64+2x8+6 =1536+256+16+6 =181410
Si utilizamos el convertidor vemos
que 34268 = 181410
Otro ejemplo
12AF a base 10
1x163+2x162+Ax16+F
1x4096+2x256+10x16+15 = 4783
Utilizando este algoritmo de las
potencias convertir:
101010101010102 a base 10
1343435 a base 10
83AF a base 10
Ahora, para convertir un número en
base 10 en una base 10, el algoritmo universal, igual que el anterior de las
potencias, sin una prueba real, excepto que funciona, es el de las divisiones sucesivas.
Ejemplo, convertir 65 a binaria.
Hacemos divisiones sucesivas
65 │2
1 │32│2
0 │16│2
0 │8 │2
0 │4│2
0 │2│2
0│1
Comenzando con el último cociente <2 =1 y
construyendo el número con ese inicio y todos los cocientes en orden ascendentes,
obtenemos el número en base 2
6510 =65 = 10000012
Vamos a convertir 65 a base 3
65 │3
2 │21│3
0 │7│3
1 │2
El número será 21023 = 65
Ejemplo
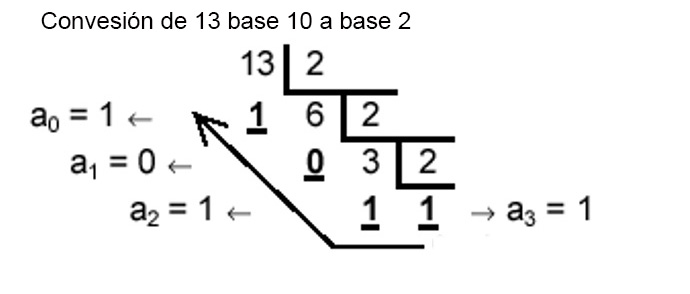
Para convertir el número 13,312510 a base 2, en primer lugar, hay que dividir, sucesivamente, la parte entera del número, en este caso (1310), entre 2, hasta obtener un cociente más pequeño que 2.
Figura 1 Convertir 13 base 10 a base 3
Como el último cociente (a3), que vale (1), ya es más pequeño que el divisor (2), hay que parar de dividir. Por tanto,
1310 = 11012
El segundo paso consiste en convertir la parte fraccionaria del número (0,312510). Para ello, se deben realizar los siguientes cálculos:
Figura 2 Algoritmo para la conversion de la parte decimal de un número en base 10
La parte fraccionaria desaparece después de
realizar cuatro multiplicaciones. Así pues, 0,312510 = 0,01012
En resumen,
13,312510 = 1101,01012
Convertir 75658 a base 8
Con el algoritmo de la división por 8, obtenemos este número en base 8
La siguiente tabla puede ayudar:
|
Número en base 10
|
Cociente entero |
Residuo < 8 |
Divisor |
|
75658 |
|
|
8 |
|
|
9457 |
2 |
8 |
|
|
1182 |
1 |
8 |
|
|
147 |
6 |
8 |
|
|
18 |
3 |
8 |
|
|
2 |
2 |
8 |
Dividimos el número en base 10 por 8, obtenemos un cociente de 9457 y un residuo menor que 8 = 2.
Dividimos el número 9457 (cociente entero anterior) por 8 y obtenemos un
cociente entero de 1182 y un residuo menor que 8 = 1.
Dividimos el número 1182 (cociente entero anterior) por 8 y obtenemos un
cociente entero de 147 y un residuo menor que 8 = 6.
Dividimos el número 147 (cociente entero anterior) por 8 y obtenemos un
cociente entero de 18 y un residuo menor que 8 = 3.
Dividimos el número 18 (cociente entero anterior) por 8 y obtenemos un
cociente entero de 2<8 y el nuevo
residuo no importa.
El número en base 8 será 223612
Se forma con el cociente < 8 y los residuos hacia atrás en orden ascendente.
Conversión de números en base a números en base b a#b y ambos enteros positivos
Aunque hay algoritmos que permiten hacer este proceso en un solo paso, ello implica que sepamos realizar las operaciones básicas y exponenciales en bases diferentes a 10.
Lo ideal es llevar el Na, al mismo número en base 10, M10
y luego llevar el número M al número Kb
Ejemplo.
Convertir el número
231234 a base 8
Por el método de descomponer el número en sus exponentes, llevamos el número en base 10
2x44+3x43+1x42+2x4+3 = 73310 = 731 operaciones hechas en base 10
Por divisiones por 8 y como se indicó anteriormente, el 731 se convierte en 13338
Ejercicios
Convertir
13567 a base 9 R 10238
567438 a base 2 R .1011101111002
33004 a base 8
R 3608
Este blog me deja una preocupación, porque no encontré ni pruebas, ni siquiera justificaciones, de que los algoritmos funcionan universalmente.
Numeración romana:
Es un sistema de numeración que usa letras mayúsculas, a las que
se ha asignado un valor numérico.
Este tipo de numeración debe utilizarse lo menos posible, sobre
todo por las dificultades de lectura y escritura que presenta.
Se usa principalmente:
- En los números de capítulos y tomos de una
obra.
- En los actos y escenas de una obra de
teatro.
- En los nombres de papas, reyes y
emperadores.
- En la designación de congresos,
olimpiadas, asambleas, certámenes...
I = 1
V = 5
X =10
L = 50
C = 100
D = 500
M = 1000
Ejemplos XVI = 16; LXVI = &&
Si a la derecha de una cifra romana de escribe otra igual o menor, el valor de ésta se suma a la anterior.
Ejemplos: VI = 6; XXI = 21; LXVII = 67
La cifra "I" colocada delante de la "V" o la "X", les resta una unidad; la "X", precediendo a la "L" o a la "C", les resta diez unidades y la "C", delante de la "D" o la "M", les resta cien unidades.
Ejemplos: IV = 4; IX = 9; XL = 40; XC = 90; CD
= 400; CM = 900
En ningún número se puede poner una misma letra más de tres veces seguidas. En la antigüedad se ve a veces la "I" o la "X" hasta cuatro veces seguidas.
Ejemplos: XIII = 13; XIV = 14; XXXIII = 33;
XXXIV = 34
La "V", la "L" y la "D" no pueden duplicarse porque otras letras ("X", "C", "M") representan su valor duplicado.
Ejemplos: X = 10; C = 100; M = 1.000
Si entre dos cifras cualesquiera existe otra menor, ésta restará
su valor a la siguiente.
Ejemplos: XIX = 19; LIV = 54; CXXIX = 129
El valor de los números romanos queda multiplicado por mil tantas veces como rayas horizontales se coloquen encima de los mismos.
Juan Fernando Sanin E
juanfernando.sanin@gmail.com