Problemas de geometría de la circunferencia - Teorema de la bisectriz

 

Jardín, Noviembre 2022

 

 

Geometría de la circunferencia (5 problemas)

1.    En la gráfica que se muestra, hallar el diámetro de la circunferencia.

Recordar la propiedad de las cuerdas que se interceptan dentro del círculo.

6x6 = x (8 + y) = 8x + xy                                           (1)

4x4 = y (8 + x) = 8y + xy                                           (2)

 

(1)  – (2)                 20 = 8x – 8y                y = (8x – 20) /8          y = x- 5/2 

que llevamos a (2)

 

2x² + 11x -72 = 0

x = (-11+√ (121+4*2*72) /4 = 3,850180                           y = 1,350189

Diámetro D = 13,70037839  

2.    En el gráfico que se muestra, hallar el radio de la circunferencia.

Encontremos las coordenadas de

B y C

<OAB = 45  deg   

AB = 2

AO = OB = √2

BC = 1                       Triángulo ABC es medio triángulo equilátero

Completemos la figura así:

< CAD = 15 deg, porque hemos construido la recta AD perpendicular a OA.

CD perpendicular a AB.      Calculemos DC           AC = √3

DC =√3sin 15 deg = 0.4482877360

La ordenada de C será igual a √2 -0.4482877360= 0.9659258263

La abscisa de C será igual √3cos 15 deg = 1.673032607

R =√ (1.673032607² + 0.965925826²) = 1.931851652

 

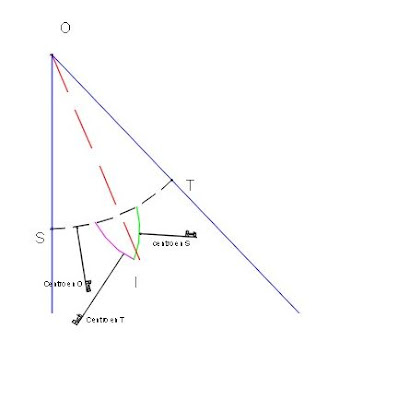
3.Trazar la bisectriz de un ángulo

 

Trazar la bisectriz de un ángulo

a.    Con centro en O se traza una circunferencia, de radio arbitrario, que determina los puntos S y T, y OS = =OT

b.    Con centro en S y con radio arbitrario m se traza otra circunferencia. Con centro en T y con el radio m, se traza otra circunferencia. El radio m debe ser tal que, las circunferencias trazadas desde S y T, se intercepten en un punto I.

c.    Se une O con. I y esa es la bisectriz.

d.    Los triángulos OSI y OTI son iguales, pues tienen los tres lados iguales. Los ángulos <SOI y <TOI son iguales, pues se oponen a dos lados iguales.

4.    Encontrar el radio del triángulo inscrito, mostrado en la figura. El triángulo rectángulo isósceles de lado 2 u. Tiene lado 2 e hipotenusa 2√2. 

 

a.  La circunferencia de la figura es el circulo inscrito, el cual encontramos trazando las bisectrices de dos de los ángulos. Las tres bisectrices son concurrentes.

b.    Ángulos <BAC y <BCA son iguales a 45 deg y los ángulos <OAC = <OCA = 22,5 deg

c.    El ángulo al centro <AOC = 135 deg

Aplicando la ley del seno

sin 135 /2√2 =sin 22.5/OA                AO = 1,530731

y

R = AO sin 22.5 = 1,530731x0,382683 = 0,585785

 

.5.    Encontrar el diámetro de la circunferencia de la figura.

 

Completemos la figura prolongando la mediatriz que pasa por C

Recordemos la propiedad, para cuerdas que se interceptan, de cualquier manera, dentro un círculo.

 

AE x EB = EC x ED

Si el radio de la circunferencia es R, el segmento ED = 2R -1

 

2x2 = 1x(2R – 1)

 

4 = 2R – 1                                        R = 5/2 = 2,5

La bisectriz de un ángulo

La bisectriz de un ángulo es el segmento de recta que divide el ángulo en dos partes iguales.

Para el caso de un triángulo:

Existen tres bisectrices (A_a, B_b y C_c), según el ángulo en el que empieza. Las longitudes de las bisectrices se calculan con la fórmula que vamos a deducir:

Primer teorema de la bisectriz

La bisectriz trazada desde A divide el segmento BC = c, en la relación:

BD/DC = AB/AC      que llamaremos

n/m = c/ b

Trazamos CE Paralela a la bisectriz AD, por paralelismos, ángulos correspondientes y alternos vemos que el triángulo AEC es isósceles y el lado igual es el lado AC = b

Por semejanza vemos BD/DC = AB/AE = AB/AC

Por tanto, BD/DC = AB/AC         n/m =c/b

Segundo teorema de la bisectriz.

La bisectriz interior se puede calcular en función de los lados del triángulo.

Veamos la demostración:

Construimos el círculo circunscrito del triángulo ABC. En la figura podemos observar:

Los triángulos AEB y ACD son semejantes, pues tienen los ángulos iguales en A y en D y C

va = longitud de la bisectriz AD

AB/AD = AE/AC       AC AB = va AD                                    (1)

bc = va (va + ED),       va² = bc –ADxDE,      va² = bc –mn                    (2)

m= ba / (b + c), n = ca / (b +c

Lo anterior debido al teorema de la bisectriz       c/n = b/m      c/b= n/m     (3)

Y Si resolvemos las siguientes dos ecuaciones:

(c + b) / b = (n + m) /m              se concluye que m = ab / (c + b) reemplazando en la ecuación m + n = a                             se concluye que n = ac / (b + c)

Con estos valores y reemplazando en la ecuación (2) obtenemos

va² = bc (b + c + a) (b + c – a) / (b + c)²

Recordemos que s = (a + b + c) /2              s – a = (b + c –a) /2 y simplificando, obtenemos

va = (2/ (b + c) √ (bcs (s –a))                                                     (2)

Vamos a transformarla.

va = (2/(b + c))√(bc(a + b + c)(b + c – a)) =2√(bc(b + c + a)(b + c -a)/(b + c)²)

va = √ (bc ((b + c)² – a²) / (b + c)²) =√ (bc [1 – a²/ (b + c)²])    (3)

(2) y (3) son fórmulas adecuadas para calcular la bisectriz trazada desde un vértice, en función de los tres lados del triángulo.

Juan Fernando Sanín E

juanfernando.sanin@gmail.com       

v