Medellín,
noviembre 2020
Aplicaciones prácticas
de la función de Lambert
Hagamos un leve repaso
del concepto de función inversa de f
Si
la función f es uno a uno, tiene inversa f-1. El gráfico 1 nos
refresca la memoria sobre este concepto.
fig 1
Consideremos
la función
f(x)=xe^x
Obviamos
el proceso para dibujar la gráfica de f(x) y presentamos su dibujo.
Dominio
de f= Reales
Rango =(-1/e, ∞)
La función no es inyectiva, lo que en teoría nos diría que no
debe tener inversa. No obstante los matemáticos han encontrado implícitamente
dos inversas para f, las funciones W-1 que corresponde a la inversa de la parte
decreciente y y Wo que corresponde a la parte creciente de f.
Las ramas W-1 y Wo se muestran en el gráfico No 3
Fig 3
El dominio y el rango de W-1 y Wo están explícitos en la gráfica
No3
No es posible hallar explícitamente la función de Lambert (W-1 y
Wo) o f-1= xex, pero se puede
construir la gráfica a partir de la´ función f(x)= xex.
En el pasado eso era muy complicado, ya que no se poseían las
herramientas computacionales adecuadas y por tanto la función de Lambert no
dejaba de ser una curiosidad matemática.
Hoy es fácil encontrar cualquier valor de W(a), con tal que a
pertenezca al dominio de W y por tanto la función ha tomado un nuevo aire en
matemáticas y física.
|
W-1 |
||
|
z |
z |
W |
|
"-1/e" |
-0,367879 |
-1,000000 |
|
-0,360000 |
-1,222770 |
|
|
-0,300000 |
-1,781337 |
|
|
-0,200000 |
-2,542641 |
|
|
-0,100000 |
-3,577152 |
|
|
-0,010000 |
-6,472775 |
fig 4
|
Wo |
||
|
z |
z |
W |
|
"-1/e" |
0,367879 |
-1,000000 |
|
-0,300000 |
-0,489402 |
|
|
0,250000 |
-0,357403 |
|
|
-0,200000 |
-0,259171 |
|
|
-0,150000 |
-0,179491 |
|
|
-0,100000 |
-0,111833 |
|
|
-0,050000 |
-0,052706 |
|
|
0,000000 |
0,000000 |
|
|
0,500000 |
0,351734 |
|
|
1,000000 |
0,567143 |
|
|
1,500000 |
0,725861 |
|
|
2,000000 |
0,852606 |
|
|
2,500000 |
0,958586 |
|
|
3,000000 |
1,049909 |
|
|
4,000000 |
1,205962 |
|
|
5,000000 |
1,326725 |
|
|
6,000000 |
1,432405 |
|
|
7,000000 |
1,524345 |
|
|
8,000000 |
1,605812 |
|
|
9,000000 |
1,679016 |
|
|
10,000000 |
1,745554 |
|
|
11,000000 |
1,806500 |
|
|
12,000000 |
1,862820 |
|
|
13,000000 |
1,915150 |
|
|
14,000000 |
1,964050 |
|
|
15,000000 |
2,009940 |
Ejemplo1
Resolver
xᶺx=3 (1)
Desarrollo
lnxᶺx=ln3
xlnx=ln3
Recordando que x=eᶺlnx, entonces
(eᶺlnx)lnx=ln3 (2)
u=lnx
La (2) queda
ueᶺu=ln3 y
W(ueᶺu) = W(ln3)
Siendo Lne>0, la rama que se utiliza de W es la Wo
Ln3=1,09861229
Wo(1,09861229) = 0,601829
Wo(ln3) se calcula en Excel, o en calculadora programable o interpolando
la tabla 2
=W(ueᶺu) = u = lnx
u = Lnx=0,601829
x=eᶺ0,601829 = 1,825454505
Ejemplo2
Resolver
eᶺx=xᶺ2 (1)
Saquemos raíz cuadrada a ambos lados
Abs(x)= eᶺ(x/2)
Si x>0 entonces abs(x)=x
x= eᶺ(x/2)
x/ (eᶺ(x/2)) =1
x eᶺ(-x/2) = 1
(-x/2) eᶺ(-x/2)= -1/2
W((-x/2) eᶺ(-x/2))= - x/2 = W(-1/2)
Pero -1/2 no está en el dominio de W-1 ni de Wo, por tanto, no
hay raíz real en este caso.
Si x<0 entonces abs(x)=-x
-x= eᶺ(x/2)
-x/ (eᶺ(x/2)) =1
(-x/2) eᶺ(-x/2) = 1
(-x/2) eᶺ(-x/2)= 1/2
W((-x/2) eᶺ(x/2))= - x/2 = W(1/2)
½ si está en el dominio de Wo
Por calculadora, o calculando por la fórmula de Newton, o
interpolando la tabla, obtenemos
W(1/2) =-x/2 = 0,35173371
Y
x= - 0,70346742
Ejemplo 3
Resolver
2x + 3lnx -3= 0 (1)
Lnx= (3 -2x)/3 =1 – (2x/3)
eᶺlnx = eᶺ(1 – (2x/3))
eᶺlnx = eᶺ1eᶺ( – (2x/3))
x/eᶺ( – (2x/3)) = e
xeᶺ (2x/3) =e
(2x/3)eᶺ(2x/3) =2e/3
2e/3>0, luego utilizamos la rama Wo
W((2x/3)eᶺ(2x/3)) =W(2e/3)
2x/3 = 0,807889
x= 1,211819
Calculo de W(x)
Otros valores de W(x) hay que calcularlos de
forma numérica, mediante el procedimiento de Newton u otros procedimientos que
convergen más rápidamente como el de Halley.
El cálculo de W(x) para un valor dado de x requiere resolver la
ecuación
transcendente, f(w)=
wew - x=0.
El método de Newton calcula la raíz de la
ecuación mediante un proceso iterativo de la siguiente forma:
Para x≥0, hay una única solución (rama Wo), el valor de partida
aconsejable es w0=1.
Para -1/e ≤x<0, hay dos posibles soluciones, para la rama W0(x)
se elige el valor de partida w0=1, para la rama W-1(x)
se elige el valor de partida w0=-2
Encontramos el valor de w, que hace f(w) = 0
f(w) = weᶺw - x
wn+1= wn − (wneᶺwn-
x)/((eᶺwn(1+wn))
f'(w) es la derivada de f(w) respecto de w. f'(w)=ew+w·ew=(1+w)ew.
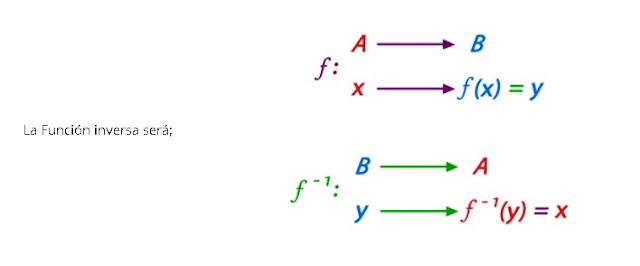




Excelente, muchas gracias.
ResponderEliminar