Jardín, junio 2024
Las Leyes de Kepler del movimiento planetario
Primera
ley: La órbita de un
planeta alrededor del Sol es una elipse con el sol en uno de sus focos.
Segunda ley: La línea que une al planeta con el Sol barre áreas iguales en tiempos iguales.
Tercera
ley: El cuadrado del
período de un planeta es proporcional al cubo de su semieje mayor.
La demostración de las tres, es un solo proceso vectorial.
La notación que utilizaremos es la siguiente:
A = (a, b) = ai + bj Las letras en negrilla representan vectores, las letras que no están en negrilla representan escalares. El valor absoluto de un vector lo denotaremos AbsA o │A│
u x v = z un vector perpendicular al plano que contiene a u y a v
F = m a De las leyes de Newton
La fuerza que hace el Sol de Masa M a la Tierra con masa m
F = - GMm/r2 u
u = r/Abs(r) = r/r y v = dr/dt (1)
F =m a = - GMm/r2 G la constante universal de la gravedad (2)
a = F/m a = -(GM/r2)u a tiene la dirección de u (3)
a = dv/dt Ver figuras 1 y 2
Para el caso de un planeta de masa m y el Sol de masa M M + m ≈ M la masa de la los planetas es despreciable, respecto de la masa del Sol. La masa del Sol es 332 946 veces más grande que la de la Tierra. M = 332946 m.
El vector h = m (r x v) momento lineal (4)
Es el momento lineal del planeta m y se conserva durante toda la trayectoria cerrada de m respecto de M.
dh/dt = d(m(r x v))/dt = m(dr/dt x v + r x dv/dt) = m(v x v + r x a )
a es vector aceleración y tiene la misma dirección de r y F , por lo tanto dh/dt = 0 y
h = c vector constante, en la dirección del vector z= u x v perpendicular al plano de u y v
h = m (r x v) momento lineal es constante en toda la trayectoria u órbita cerrada de m (5)
r depende del parámetro θ pero también es función de t (tiempo)
Figura 1. Definición de cónicas en polares. Hemos
hecho coincidir el eje polar con el eje x y que además, este eje contiene el
foco o focos de la cónica. Si e<1
la cónica es una elipse, si e = 1 es una parábola y si es >1 es una
hipérbola.
Figura 2.
Ubicación del eje polar, del foco, de la
directriz, vectores unitarios u, w y v
El ángulo θ es positivo si se mide en sentido antihorario y negativo si se mide en sentido horario.
r(θ) = r(θ) u
u = (cos θ, senθ) = cosθ i + senθ j
w = (-senθ, cosθ) = -sen θ i + cosθ j
u y w son unitarios y perpendiculares entre si u. w = 0
du/dt = (du/d θ) (dθ/dt) = (-cos θ, sen θ) dθ/dt = w dθ/dt (5a)
De igual forma encontramos que:
dw/dt = - udθ/dt
(5b)
Elegimos un sistema de coordenadas polares, tal que: enel tiempo t = 0, θ = 0, el eje polar contiene el foco o focos de las orbitas y además, el r mínimo (Perihelio = posición más cercana del planeta de masa m) está más cercano del Sol.
dr/dt (0) = 0
Trabajemos con la velocidad:
v = dr/dt = (d (r u) /dt) = rdu/dt + udr/dt (5c)
a(t)= d (rdu/dt + udr/dt) dt
= r(dθ/dt) (dw/dt) + w {(rd2 θ /dt2) + (dθ/dt) (dr/dt)} + (dr/dt) (du/dt) + ud2r/dt2)
= r(dθ/dt) (-u dθ/dt) + w {(rd2 θ /dt2) + (dθ/dt) (dr/dt)} + (dr/dt) (wdθ/dt) + ud2r/dt2)
= r(dθ/dt) (-u dθ/dt) + w {(rd2 θ /dt2) + (dθ/dt) (dr/dt)} + (dr/dt) (w dθ/dt) + ud2r/dt2)
= -r(dθ/dt)2u + r(d2θ/dt2) w + 2(dθ/dt) (dr/dt) w + (d2r/dt2) u
Pero a = -(GM/r2) u Que implica que, el componente de w tiene que valer 0
0 = rd2θ/dt2 + 2(dr/dt) (dθ/dt) (6)
Y la aceleración será: a(t) = (-r(dθ/dt)2 + d2r/dt2) u (7)
Si la (6) la multiplicamos por r quedará así:
r2d2θ/dt2 + 2r(dr/dt) (dθ/dt) = 0 (7a)
Veamos cuál es la derivada de la función f = r2(dθ/dt) d{(r2dθ/dt)/dt}
La derivada es d{(r2dθ/dt) /dt} = r2d2θ/dt2 + 2r(dr/dt) (dθ/dt), que sabemos por (7a) que es igual a 0, lo que implica que la función:
f = r2(dθ/dt) es constante. (8)
Si A(θ) = (1/2) ∫r2dθ
Y dA(θ) = (1/2) r2 dθ
dA(θ)/dt = (1/2) r2 dθ/dt = K Constante (9)
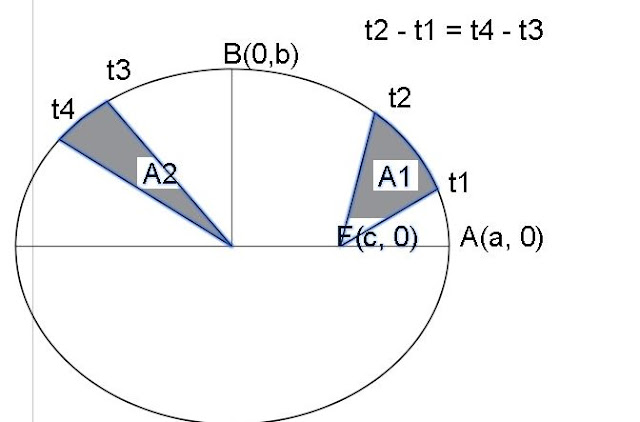
Figura 3. : La línea que une al
planeta con el Sol, barre áreas iguales en tiempos iguale
Si [t1, t2] y [t3, t4] son tales que t2 – t1 = t4 – t3 t
A = K [t2 – t1] = K [t4 -t3] Luego, la línea que une el planeta con el Sol, barre áreas iguales en tiempos iguales.(Queda demostrada la segunda ley de Kepler)
Sigamos con la demostración de la primera ley de Kepler
-GM/r2 = -r(dθ/dt)2 + d2r/dt2 Por la (7) (10)
De la (8) tenemos
r2dθ/dt = Cte dθ /dt = Cte/r2 = H/r2 H es una constante importante (11)
El momento lineal de m h = mr (u x v) en el tiempo t y ángulo θ
Recordemos:
v = r(dθ/dt) w + u (dr/dt)
h = m [ru x (r(dθ/dt) w + u (dr/dt))]
h= m(r2dθ/dt) uz + mr(dr/dθ) u x u) = mr2(dθ/dt) uz uz perpendicular al plano de u y v
Abs h = mr2(H/r2) = mH dθ/dr = H/r2 (12)
H = Abs(h)/m
mr2 (dθ/dt) = mH dθ/dt =H/r2 = dθ/dt = Hw2 Ver def/ de w (12a)
Sea w = 1/r (13)
Este w no tiene nada que ver con el vector w, es sólo un cambio de variable.
dr/dt = (dr/dw) (dw/dθ) (dθ/dt) = (-1/w2) (dw/dθ) (Hw2) = -(dw/dθ) H por (11)
a(t) = d2r/dt2 = (-Hd[(dw/dt)]/dt Aplicar la regla de la cadena, parece difícil.
Ayudémonos:
w = f(θ)
w’ = f’(θ) = dw/dθ
w” = f” (θ) = d2w/dθ2
Por tanto
-(Hd(f’(θ)) /dt = -Hf” (θ) dθ/dt = H (d2w/dθ2) (dθ/dt) =
a(t) = d2r/dt2 = -H.H w2 d2w/dθ2 = -H2w2d2w/dθ2 ya que: dθ/dt = H/r2 = Hw2 por la (12a)
La (10) la transformamos en -GM/r2 = -r(H/r2)2 – w2H2(d2w/dθ2)
-GM/r2 = -r(H/r2)2 – w2H2(d2w/dθ2)
-GMw2 = -w3(H)2 –w2H2(d2w/dθ2)
-GM = -wH2 - H2d2w/dθ2
GM/H2 = w + d2w/dθ2 k1 = GM/H2
w” + w – k1 = 0 ecuación de segundo orden y primer grado (14)
y = w - k1
w = y + k1
y” + y = 0 (14a)
La solución de esta ecuación diferencial es y = Acosθ + Bsenθ. Favor verificarla
Derivando se puede chequear que la ecuación 14a se cumple. Cambiando y por w - k1
w” + w – k1 = 0 k1 = GM/H2
Esta ecuación es equivalente a: w = C cos(θ – α) + GM/H2
w = C [cosθ cosα + senθ senα) + GM/H2 Constantes C y α A = Ccosα B = C senα
Si hacemos coincidir el eje polar con α= 0
w= Ccosθ + GM/H2
r = 1/ (Ccosθ + GM/H2) = H2/ (H2 C(cosθ) + GM) = (H2/GM) /[((H2Ccosθ) /GM) + 1)
sí e = H2C/GM y p = 1/C
r=ep/(ecosθ+1) (15)
que es la ecuación de una cónica en coordenadas polares, con origen en el foco y eje polar que contiene el foco, y es horizontal (eje x)
0<e<1 la cónica es una elipse
e= 1 es una parábola
e > 1 una hipérbola.
Para el problema del movimiento de los planetas, tratándose de una trayectoria cerrada, la órbita, obligatoriamente, tiene que ser una elipse.
Recordemos la segunda ley de Kepler
r2 (dθ/dt) = Cte e igualmente dθ/dt = H/r2 H =r2 dθ/dt y además, por la (12)
Abs h = mH
Siendo dA/dt = Cte, se puede establecer que el área recorrida en el periodo T (Completo), para el caso de la Tierra T = 1 año
dA = (1/2) r2 dθ dA/dt = (1/2) r2 (dθ/dt) dt
dA = (1/2) H dt y en t = T = año, el área barrida será:
pab = (1/2) HT (15a)
En θ = 0 r = a – c = ep/ (1 + e)
En θ = p r = a + c = ep/(1 – e)
Figura 4. Elipse: Ejes cartesianos x e y, semiejes
a y b, distancia focal c. Ejes polares con centro en el foco F1 y eje polar en
la dirección del eje x.
Deducimos que:
a = ep / (1 – e2)
c= e2p / (1 – e2)
b = √ (a2 – c2) = √ (a2 – (ae)2) = a√ (1 – e2) recordar del blog cónicas que e = c/a
De (15a) T = 2pa2√(1 – e2)/H elevando al cuadrado
T2 = 4p2a4(1 – e2) /H2 = 4pa3a (1 – e2) /H2 = {4pa3[(ep)/ (1 – e2)] (1 – e2) /}H2 ep= (H2Cp/(GM))
T2 = 4p2a3 /(GM) = 4p2a3/(GM) = Ka3 (16)
Cp = 1 ver definición e = H2C/(GM) p = 1/C
H2 =GMep
K = 4p2/(GM) = 3x10 -19 seg2/m3
Si en vez de metros, utilizamos AU (Unidades
astronómicas, 1 AU = 150 millones de km) y en vez de segundos, utilizamos años
terrestres (1 año = 3600x24x365 segundos), la constante K será igual a 1 K = 1 años 2/ (AU)3
G constante de la ley de la gravedad de Newton G = 6.67 x 10-11 N m2 /kg2 = 6.67x 10 11 m3 / (kg sec2)
M masa del Sol = 1.99 x 10 30 kg
mtierra = 5.96 x 1024 kg
Relación masa del Sol / masa de la Tierra = 333000
La masa del Sol es más del 99,8% de la masa de todo el sistema solar conocido
Datos Planetarios.
Tablas de propiedades planetarias.
Debemos aclarar que es una AU (Unidad Astronómica)
Unidad astronómica (UA) es una unidad de distancia que vale a 149.597.870,66 kilómetros (150 millones de km). Es aproximadamente igual a la distancia media entre la Tierra y el Sol
Un Parsec es la unidad de medida de distancia equivalente a unos 3.26 años luz, o 3,09 × 1016metros = 3,09 x 1013 km
El año luz es la distancia que recorre la luz en un año y equivale a 9,46 millones de millones de kilómetros. Esta unidad es muy útil para expresar las distancias entre cuerpos estelares.
Nos han contado que la distancia Tierra – Sol, fue
descubierta, de manera aproximada, desde los griegos, lo cual no parece ser
cierto.
Hoy hay serias dudas sobre la realidad de la teoría atómica, al igual que de la teoría de la relatividad, incluso sobre la fuerza de la gravedad.
Yo veo este blog, como una aplicación de cálculo y mecánica celeste. El cálculo es difícil que cambie, pero la mecánica celeste si es susceptible de renovación de teorías y tal vez sea pronto.
Muchos de los datos planetarios que se muestran en la tabla, parecen cuadrados para que la teoría de la gravedad funcione o viceversa.
La estrella más cercana al Sol se llama Próxima Centauri y se encuentra a 4,22 años luz y cada año luz mide 9,46x 10 12 km.
Investigando en Google, cuál ha sido la mayor velocidad de un cohete producido por el hombre, que utilice combustible conocido hoy, encontramos cifras dispersas y no coincidentes. Encontramos 39420km/h, o 45000 km/h y la máxima que encontré fue de 50536 km/h
El tiempo que tardaría una nave o cohete tripulado, con estas velocidades, para ir de la Tierra a Próxima Centauri sería:
4,22x 9,46x 10 12 km./ 50536 km/h = 7,89x 10 8 h = 7,89x 10 8 /(24x365) años
90000 años ¿????????????? Estamos encerrados.
Una bala de un super fusil, el mejor, viaja a 1,2 km/sec = 4320 km/h
4320<<50536 Lo cual me hace dudar también de los datos de velocidad de los cohetes hoy.
Atentamente,
Juan Fernando Sanín E