Medellín, noviembre 2023
Blog funciones: ln(x), ex - y determinación del número e
Generalidades
Consideremos la función y = 1/t, y su gráfica, para valores de t>0
Fig 1 definición de la función ln(x)
Si encontramos el área debajo de la curva y = 1/t, entre t=1 y un valor arbitrario de t, t=x, x>0, esa área es creciente, en la medida que, cuando vamos aumentando el valor de x ,hasta el valor que queramos, el área continuará creciendo. Por lo tanto, podemos afirmar que la función definida como:
Es creciente en todo su dominio t>0
Esta función tiene unas propiedades interesantes:
Es creciente en todo su dominio t>0
1.) ln(xy) = ln(x)+ln(y)
2.) ln(xn) = nln(x) para n entero positivo

ln(xn)= n*ln(x) que, también es otra propiedad de los logaritmos, en cualquier base. Podemos extender esta propiedad para cualquier n que sea Real. (La demostración no es fácil)
3.) ln(x/y) ln(x) -ln(y) (5)
ln(x/y) = ln((x)(y-1))= ln(x) + ln(y-1) = ln(x) - ln(y)
y = ln(x) implica que: ey=x o e ln(x) = x
Fig
2 ln(x) = loge(x)
Derivada de ln(x)
Sea y = ln(x)equivalente a:
ey = x
Diferenciando implícitamente a ambos lados obtenemos:
eyy’ = 1 de donde: y’ = 1/ey = 1/x
ln’(x) = 1/x (6)
B. El número e
Por integración aproximada podemos encontrar ln2,5 y ln3
ln(2) =0,69
ln(3) =1,09
El número e es un número real entre 2 y 3, ya que la función ln(x) es monótonamente creciente.
Pero ese no es e. e es un irracional de infinitas cifras, similar a p
Euler resolvió el problema, por medio de este límite:
Si hacemos x= 10 y calculamos (1+1/10)10 encontramos un valor aproximado de e
Si hacemos x= 100 y calculamos (1+1/100)100 encontramos un valor mejor que el anterior.
Con la paciencia del caso, esta fue una de las formas de calcular e
Con 10 cifras exactas, el valor de e es igual a e = 2,7182818284
Con la serie de Taylor para ex, también podemos calcular el valor de e.
Esta
suma la podemos calcular con 10, 11, 100 sumandos y más. Y Ahora con las
computadoras podemos usar 1000 sumandos o más.
Función exponencial natural y = ex
El dominio es (-∞, ∞)
El
rango es (0, ∞)
La
derivada es y’ = ex >0; para todo x real, por lo que la función
es monótonamente creciente en todo su dominio.
Veamos este ejemplo:
ln3,5 = 1,2527629684953679956881206
e
1,2527629684953679956881206 = 3,5
Claramente vemos que e ln(x) = x y que, las funciones lnx y ex , son mutuamente inversa. Sus gráficas son simétricas respecto de la recta y = x
Equivalencia de un logaritmo en una base e, ln(x) a un logaritmo en una base cualquiera a
Sea y= logax y1 = logb x
Por tanto, x = a y x = b y1
Se concluye que, a y = b y1
Tomando logaritmo en base a de la igualdad anterior:
ylogaa = y1logab como logaa = 1 y = y1logab
Reemplazando logax = logbx*logab y
logbx = logax/logab (9)
si b =10 base de los logaritmos vulgares a = e base logaritmos naturales
log10x = log(x) = loge(x)/loge(10)
log(x)
= ln(x)/ln10
(10)
¿Cómo calculamos el lnx?
Hay varias series infinitas de Taylor y Maclaurin que, nos permiten calcular el ln(a) para cualquier valor de a real.
Ln[(1+x)/(1-x)]
= 2[x + x3/5+ x5/5+………………….+x 2n-1/(2n-1)
+….] -1<x<1 (11)
Ejemplo
ln12,3 12,3 =(1+x)/(1-x)
12,3-12,3x =1+x x=11,3/13,3 =0,849624
Vemos que este valor está en el intervalo de convergencia, (-1, 1), por tanto, aplicamos la fórmula (11) con x = 0,849624 y utilizamos la serie (11), con suficientes términos para garantizar una precisión determinada y eso lo enseña el conocimiento de las series deTaylor y Maclaurin y el teorema del residuo.
Ejercicios:
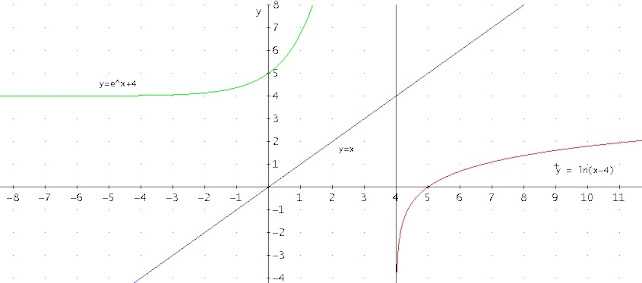
1. Hallar la función inversa de y = ln(x-4)
Vemos que el dominio de la función es el intervalo (4, ∞) y el rango (-∞, ∞)
Despejamos x ey = x-4 x=ey+4 ahora intercambiamos x e y
La función inversa será y = ex+4 Cuyo dominio son todos los Reales y cuyo rango es:
(0, ∞)
1.
Ejercicio 2
Simplificar ln25+ln40-3ln10
=2ln5+ln5+ ln8 - 3ln2-3ln5
=0 +3ln2-3ln2 = 0
El
valor absoluto de x, nos asegura la existencia de la integral para todos los
reales.
Aplicaciones de la función exponencial natural
La función exponencial neperiana y =ex, tiene aplicaciones en la estadística y en la ciencia.
Sea y una variable que crece o decrece con el tiempo. Además, la tasa de variación de la variable y es proporcional al valor de la función y en el tiempo t.
y crece con el tiempo y además, dy/dt = ky
dy/y = kt
Integrando, obtenemos la fórmula y = Cekt t= 0 y = yo y por tanto C = yo
y = yoekt (12)
Conocido yo, debemos obtener el valor de k, el cual se consigue con otro dato conocido de la variable y.
Ejercicio
El 30% de una sustancia radioactiva, se desintegra en 15 años, después de que la sustancia se saque del laboratorio. Determinar la semivida de la sustancia.
y = porcentaje de la sustancia que no se ha descompuesto en el tiempo t (años)
y=yo ekt k es la constante de decrecimiento.
En el tiempo t= 0 años, y es igual a 100%, mejor digamos que es igual a 100
En
el tiempo t= 15 años, y es igual a 70%, mejor dicho y = 70
La vida media, es el tiempo en el cual la sustancia se ha reducido a la mitad. y= 50% , y=50
70=100e15k
15k = ln0,7 k = -0,023778
Ahora
50 = 100e(-0,023778*t) y el t de esta ecuación es la vida media del elemento.
-0,023778t =ln(1/2) = -0,693147 t = 29,15 años
Juan
Fernando Sanín E
juanfernando.sanin@gmail.com








No hay comentarios:
Publicar un comentario