Jardín, septiembre 2022
La pregunta básica que
se me ocurrió, desde que me enseñaron las series de Fourier, es como se
demuestra que la fórmula básica, que veremos más adelante, realmente representa
la función en el intervalo escogido. Ni mi profesor supo explicarme y tampoco
he encontrado respuesta convincente en los libros de ecuaciones diferenciales
que he consultado.
2. Función par e impar
Ejemplos f(x) = x^2; f(x) = cos x (sabemos que cos(x) = cos(-x)
Función f es impar si se cumple que f(x) = -f(-x) (nos indica simetría, respecto del eje origen)
Ejemplos f(x) = x^3; f(x) = sin(x) (sabemos que sin(x) = -sin(-x)
En el caso de las funciones impares, periódicas, con un periodo T la integral definida entre -T/2 y T/2 de f(x) es igual a 0, porque las áreas donde la f es positiva, es igual al área donde la función es negativa.
Si f es par y g es par, h(x) = f(x)g(x) también es par; h(-x) = f(-x)g(-x) = f(x)(x)= h(x)
Si f es par y g impar, h(x) = f(x)g(x) es impar h(-x) = f(-x)g(-x) = f(x)(-(g(x)) = - f(x)g(x)= -h(x)
Igualmente, si f es impar y g es impar entonces h(x) es par
Además, sin(np)=0 si n pertenece a los enteros
cos(np) = (-1) ^n para todo n que pertenece a los enteros.
3. Fórmula de la serie de Fourier, aplicada a funciones periódicas, periodo T = [-p, p]
Sea f(x) una función periódica, definida en el intervalo [-p, p], esta función se puede representar de la siguiente manera:
Las ecuaciones (1) a (4) permiten desarrollar expresiones que se aproximen
a funciones periódicas, definidas en el intervalo [-p, p]
Antes de hacer un ejemplo, que nos permita utilizar las fórmulas (1) a (4), para desarrollar funciones periódicas de acuerdo con Fourier, hay una tabla pequeña de integrales, que se utiliza en ejercicios de la serie de Fourier.
Ejemplo 1
f(x) = {-1 si -p<x<0
1 si 0<x<p (5)
(Función definida por trozos o tramos) Ver gráfica en la figura 1 en rojo en periodo [-p, p]
Figura 1 Aproximación en serie de Fourier, de la función definida en (5)
Lo primero que debemos analizar es si la función es par o impar o no entra en esta clasificación.
En este caso la función por trozos es impar f(x) = -f(-x) (además, se ve la simetría
respecto del origen.
Veamos la serie de
Fourier y calculemos sumas parciales S1a S9
Como se puede ver en la
gráfica de la figura 1, ya S9 está marcando una tendencia y la parte casi
horizontal de la serie, se va ajustando a la función por trozos definida en el
ejemplo 1.
Si pudiéramos llegar a
S100, ya prácticamente la función definida por la serie estaría acomodada sobre
la función definida a trozos.
Ejemplo 2
f(x) = {p+x si -p<x<0
x si 0<x<p
Figura 2
La función periódica en estudio no es par ni impar. El periodo es [-p, p]
Debe tener coeficientes ao, an y bn
El valor de p en la fórmula general es p = p
Podemos calcular S8,
S100 y mientras más grande sea n, la serie se aproxima más a la función.
En la gráfica de la
figura (2) ya vemos que S6 se aproxima bastante a la función con la que hemos
tratado en este ejemplo.
Ejemplo 3
Sea la función f(x)= x sólo en el intervalo [-p, p]
Esta función es impar, por tanto, en el período T = 2p
Al ser impar, ao y an son iguales a 0.
Sólo calcularemos a bn
Utilizamos las fórmulas
de integrales útiles en el tema de Fourier
S2=
- (2p/1) sinx+(2p/2) sin(2x)
S3= - (2p/1) sinx+ (2p/2)
sin (2x) -(2p/3)
sin(3x)
S4= - (2p/1) sinx+ (2p/2)
sin (2x) - (2p/3)
sin(3x) + (2p/4)
sin(4x)
S5= - (2p/1) sinx+ (2p/2)
sin (2x) - (2p/3)
sin(3x) + (2p/4)
sin(4x) - (2p/5)
sin(5x)
Figura 3 f(x) representada por S5 de la serie de
Fourier.
Si en vez de S5, llegáramos a S10, la aproximación sería mucho mejor.
Para terminar, ni me enseñaron, ni he encontrado en los libros de ecuaciones diferenciales que, he consultado, una respuesta razonable para la validez de la ecuación (1)
Juan Fernando Sanín E
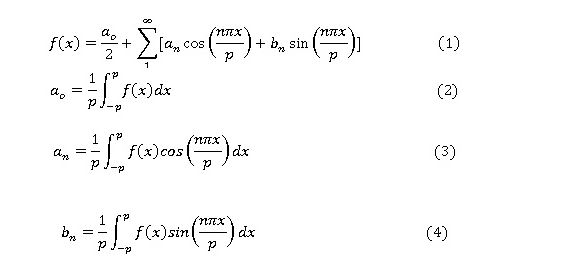








No hay comentarios:
Publicar un comentario