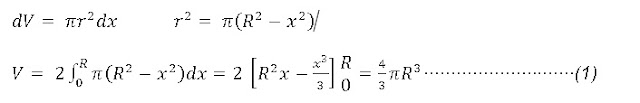Medellín, septiembre
2023
Arquímedes vs Newton: Área y Volumen de la esfera de radio R
Volumen de la estera de radio R
Llegar a este resultado, después de Newton y Descartes, es muy fácil, pero se pregunta: ¿cómo los griegos llegaron a esta fórmula, sin la ayuda del cálculo? Igualmente, pasa con la fórmula del área lateral A= 4pR2
Comencemos con la fórmula para el volumen de la esfera de radio R
r=√(R2-x2)
Figura 1
De igual manera, el cálculo integral, nos dio el medio, para hallar el área lateral de la esfera
Figura 2
x2 + y2 = R2
y = √(R2 - x2) x>0 y>0 sólo un cuarto de circunferencia
ds = √(1+(dy/dx)2) dx 0 ≤ x ≤ R [0, R]
r =√(R2-x2)
dA = diferencial de área del anillo que se muestra en la figura (2)
dA =2prds =2p√ (R2- x2) ds = 2p√(R2-x2) √(1+(dy/dx)2) dx x en el intervalo [0, R]
dy/dx = -x/√ (R2 - x2) (dy/dx)2=x2/(R2 - x2)
dA =2p√ (R2 - x2) √(1+(x2/(R2 - x2))=2pRdx
Cuando vivía
Arquímedes, no existía el cálculo. Cómo hizo
Arquímedes para llegar a las fórmulas del volumen y del área lateral de una
esfera E?
Para el caso del volumen, su razonamiento fue extraordinario.
Alineadas horizontalmente, como se indica en la figura (3), Colocó una semi esfera de radio R, un cono de radio R y altura R y un cilindro de radio R y altura R.
El observó que, para cada sección horizontal, que cortara los tres sólidos, el área de la sección de la semi esfera + el área de la sección del cono era igual al área de la sección del cilindro
Consideremos un plano horizontal, ubicado a una altura x (como se muestra en la figura (3))
Figura 3
Semi esfera, cono y cilindro
A la altura x, mostrada en la figura (3:)
El área de la sección de la esfera a la altura x es = p(√(R2-x2))2 = pR2 – px2
El área de
la sección del cono, a la altura x será = px2 el radio es x
Sumo estas
dos áreas y el resultado es: p (R2-x2) + px2
= pR2 que
es el área de la sección del cilindro a la altura x
Veamos que
el área de la sección de la semi esfera =área cilindro – área del cono.
Cuando x =0 pR2 = pR2
- 0
Cuando x = R/2 p(√(R2-(R/2)2)2 = (3/4) pR2 = pR2 - p(R/2)2 = (3/4)
pR2
Cuando x =
R 0
= pR2
- pR2
Teniendo en cuenta el razonamiento anterior, Arquímedes concluyó que el Volumen de la semi esfera es igual a:
Vol Semi Esfera = Volumen del cilindro – Volumen del cono = pR3 - pR3/3 = (2/3)pR3
Y el volumen de la esfera completa es V = (4/3)pR3 (1)
Para el caso del área de la esfera, la intuición de Arquímedes fue aún más intensa y fuerte.
Inscribió una esfera de radio R en un cilindro de radio R y altura 2R, como se ve en las figuras (5) y (6)
Fig
5
Figura 6
Por tanto, si sumamos
todas las áreas de las cintas esféricas, tales que ds sea tan pequeña como
queramos, la suma de estas áreas será igual a la suma de las áreas de las
cintas cilíndricas, siempre y cuando k sea muy pequeña (Consecuente con ds muy
pequeño). La suma de las áreas de las cintas cilíndricas es el área lateral del
cilindro: 2pR*(2R)
= 4pR2
Por tanto, el área de la esfera es igual a A = 4pR2
Según cuenta la leyenda, Arquímedes, pidió que en su lápida, se dibujaran las gráficas que le permitieron calcular el área y el volumen de la esfera, especialmente la de la esfera de radio R, inscrita en el cilindro de radio R y altura 2R. Arquímedes 287 BC a a 212 BC
Juan Fernando Sanin E