Jardín, febrero 2021
Solución de
ecuaciones diferenciales por medio de la Transformada de Laplace
Siempre que estemos ante una ecuación diferencial, lo primero que
debemos intentar es separación de variables; es decir, después de las
simplificaciones algebraicas, llevar la ecuación a una expresión como:
h(y)dy = g(x)dx
Y luego se resuelve por integración.
No obstante, aunque gran parte de las ecuaciones diferenciales que
aparecsen en física e ingeniería, terminan siendo de este tipo (separación de variables),
hay mucho tipo de ecuaciones diferenciales, en las cuales no es posible esta
simplificación.
Uno de esos múltiples tipos de ecuaciones diferenciales, no
separables, son las llamadas ecuaciones
diferenciales lineales con coeficientes constantes, como se indica en la
ecuación (1).
Anyn+An-1yn-1+………….
+A1y’+Aoy+B=0
(1)
Transformación (transformada) de Laplace de una función.
f(x) está
definida para todos los puntos 0<x< ∞
f(x) es continua o continua a trozos, en cualquier intervalo 0 < x
< b.
f(x) es de orden exponencial a,
lo cual significa que, para todo x, A y a reales
│f(x)│<Aeax
La Transformada de Laplace de una función f(x) con
las características arriba indicadas se define como:
Así definida, como una integral, la transformada de
una función f(x) cumple las típicas propiedades de linealidad:
L(f(x)+g(x))=L(f(x))+L(g(x))
L(cf(x))=cL(f(x))
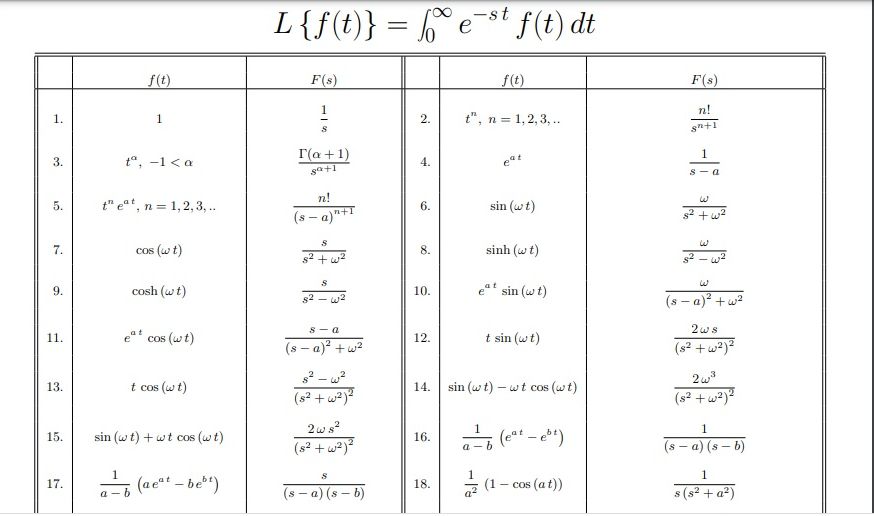
Tablas de Transformada de Laplace
(x o t no importa el nombre de la variable de la
función f. Si es importante tratar de llamar la función transformada F como
F(s)
Tabla 1
Implícitamente, queda definida la
función L-1, que debe cumplir la propiedad de las funciones inversas:
L-1(F(s)) =f(x) si x es la variable principal de f
L-1(L(f(x)) =f(x)
No vamos a definir L-1;
sólo utilizaremos la tabla para encontrar L-1 partiendo de L y L
partiendo de L-1
Ahora si veamos,
cómo funciona este método. (Sólo para ecuaciones diferenciales del tipo (1) ) y
se reduce a aquellas con una limitación adicional y es que los puntos en los que
se conocen la función y sus derivadas, deben ser en x = 0.
¿Cómo funciona?
1.
Ejemplo 1
y’’-2y’-3y=1
(3)
y (0) =1
y’(0)=-1
A la ecuación (3) le aplicamos la
transformada de Laplace
L(y’’-2y’-3y) =L (1)
L(y’’) +L(-2y’) +L(-3y) =L (1) aplicando la
propiedad lineal
L(y’’)-2L(y’)-3L(y)=L (1)
Vamos a la tabla:
s2F(s)-sf(0)-f’(0)-2(sF(s)-f(0))-3F(s)=1/s
s2F(s)-s+1-2(sF(s)-1)-3F(s)=1/s
F(s)(s2-2s-3) =(1/s)-3+s
F(s)=(s2-3s+1)/(s(s-3) (s+1))
Esta es una fracción polinómica propia.
(grado del numerador 2 < grado del denominador 3). Esta fracción se puede
separar en fracciones parciales así:
(s2-3s+1)/(s(s-3) (s+1))
=A/s +B/(s-3) + C/(s+1) =(A(s-3) (s+1) +s(-2A+B-3C) – 3A)/(s(s-3) (s+1))
Reducimos a común denominador el lado
derecho. Las fracciones de izquierda y derecha quedan con igual denominador y
son iguales. Los numeradores (polinómicos) también serán iguales y así podemos
determinar A, B y C
Coef de s2 A + B + C =1
Coef de s
-2A + B -3C =-3
Termino independiente -3A = 1
A=-1/3
B=1/12
C=5/4
F(s) = -1/(3s) + (1/(12(s-3)) +5/ (4(s
+1))
Y aplicamos L-1 y utilizando las
propiedades de la linealidad:
L-1(F(s)) =-1/3 L-1(1/s) +(1/12) L-1(1/
(s- 3)) + (5/4) L-1(1/ (s + 1)) = f(x)
f(x) = -1/3 + (1/12) e3x +
(5/4) e-x
Podemos chequear si llegamos bien a
f(x), recordando f (0) =1
f(0) = -1/3 + (1/12) e0 +
(5/4) e0= -1/3 + 1/12 + 5/4 = (-4+1 +15) /12 =12/12 =1,
que era uno de los datos. y(0)=1
Ejemplo 2
el problema: y’ – 2y = 2x + 1 (4)
que satisface y
(1) =2 :
Puesto que las
condiciones no son en x=0, lo que hacemos es un cambio de variable y corrimiento de la forma x
= t+ a
Donde t es
una nueva variable independiente; lo que requerimos es que cuando t=0 coincida
con x=1, para ello cambiamos:
x=t +1 o t = x -1
Con este cambio
el problema inicial se cambia por:
y’ – 2y = 2(t +1) + 1 = 2t + 3
que satisface:
x=1, t=0, y (0) =2 Aquí hablamos de y=2, cuando t = 0,
Y ahora si, continuamos con la metodología del ejemplo anterior: Aplicando la transformada en ambos miembros tenemos:
y’ – 2y = 2t + 3 (ahora la función y es de t y no de x)
L (y’ – 2y) = L (2t + 3)
L(y’) – 2L(y) = 2L(t) + 3L (1)
sF(s) -f (0) -2F(s) = 2/s2 + 3/s de acuerdo con las fórmulas de la tabla (1)
sF(s) -2 -2F(s) = 2/s2 + 3/s
Despejamos F(s)
F(s) = (2 + 3s +2s2)/((s2(s – 2))
(5)
F(s) = A/(s – 2) + B/s + C/s2
(As2 + Bs(s – 2) + C(s -2))/ ((s2(s
– 2)) (6)
Igualamos los numeradores son iguales:
Por tanto:
-2C=2 C=-1
-2B + C =3 B=-2
A + B =2 A = 4
Veamos L-1(1/s2)
La fórmula (5) de
la table L(tneat)
= n! / (s -a) n+1
Para este caso a = 0
y n = 1
L-1(1/s2) = t
L-1(F(s)) = g(t) = 4e2t – 2 – t
Recordemos
que x =t + 1 por tanto t=x -1. Al cambiar t por x, g(t)
se nos convierte en f(x), que es la que estamos buscando.
f(x) = 4e 2(x
– 1) – 1 – x
Conclusión
El método de Transformada
de Laplace, para resolver ecuaciones, es muy limitado y se reduce a ecuaciones
de la familia de la ecuación (1), con una limitación adicional, y es que los
puntos que se conocen, deben ser en x = 0
Se deben conocer
f’’ (0), f’ (0) y, f (0). Cuando las condiciones no se dan en x=0 hay que hacer
un cambio de la variable x por otra t, de
tal manera que podamos conocer los valores de g’’(t), g’(t) y g(t) en t = 0
Finalmente
recordemos que hay una diferencia entre F y f
F(s) = L(f(t))
Nota: Sin
pretender hacer un repaso de la materia “Ecuaciones Diferenciales”, en los
próximos blogs voy a tratar el tema de las ecuaciones diferenciales lineales y
de las homogéneas y no homogéneas, exactas e inexactas.
Juan Fernando Sanin E

No hay comentarios:
Publicar un comentario