Transformaciones lineales II (2 de 2)

Medellín Marzo 2011

TRANSFORMACIONES LINEALES II

Continuando con este tema, resolvamos el siguiente problema:

T: V→W

T: R3→R3

T(x, y, z) = (x + z, y + z, x + 2y + 2z) Todo en los reales.

Verificar si los vectores (1, -1, 0) ^T y (2, -1, 3) ^T están en la imagen de T, imT.

Una base para R3 es {i, j, k}

Encontremos las transformadas de estos vectores:

T (1, 0, 0) = (1, 0, 1) ^T, T (0, 1, 0) = (0, 1, 2) ^T, T (0, 0, 1) = (1, 1, 2) ^T

El seudoexponente T significa transpuesto.

La matriz de transformación A_3x3 está formados de tal manera que sus columnas son los vectores (1, 0, 1) ^T, (0, 1, 2) ^T y (1, 1, 2) ^T

Recordemos la fórmula: ρ (T) + v (T) = 3 = número de columnas de A.

Para encontrar el núcleo nu(T) resolvemos el sistema Ax = 0

x+ z = 0

y + z = 0

x + 2y + 2z=0

Este sistema se puede reducir a:

x+ z = 0

y + z = 0

x=0

Con lo cual su única solución es la trivial, o sea el vector (0, 0, 0) y por tanto su núcleo es el vector (0, 0, 0) y su nulidad es v (T) = 0

Por tanto: ρ (T)=3

Como el rango es 3, los vectores (1, 0, 1) ^T, (0, 1, 2) ^T y (1, 1, 2) ^T

Forman una base para R3 y por tanto, la imagen de T im(T) = R3 y por consiguiente, cualquier vector en R3= W es una transformada de algún vector en R3= V, y se concluye que la respuesta al problema es que los vectores:

(1, -1, 0) ^T y (2, -1, 3) ^T

Si están en im(T).

No obstante, para repasar algunos conceptos hagamos la siguiente discusión:

Det A = -1 por tanto, la matriz A tiene inversa.

Por cualquiera de los métodos encontramos A ^-1 la inversa de A (Descrita arriba)

A ^-1 es la matriz cuyas columnas son (0, -1, 1) ^T, (-2, -1, 2) ^T y (1, 1, -1) T

Si Ax=y entonces x=A^-1y

Los vectores x en V se convierten en vectores y en W por A y los vectores y en W se convierten en vectores x en V por A^-1. Aplicando estas transformaciones al vector (1, -1, 0) ^T

A^-1 (1, -1, 0) ^T = (2, 0, -1) ^T

Y

A (2, 0, -1) ^T = (1, -1, 0) ^T

Con el segundo vector

A^-1 (2, -1, 3) ^T = (5, 2, -3) ^T

Y

A (5, 2, -3) ^T = (2, -1, 3) ^T

Por tanto, se ratifica la respuesta, los vectores indicados si están en la imagen de T.

TRANSFORMACIONES LINEALES EN R2

T(x, y) =(-y, x)

Esta transformación toma un punto o una figura en R2 y la rota 90º en sentido positivo (antihorario).

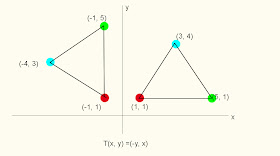
Figura 1

T(x, y) =(y, x)

Esta transformación toma un punto o figura en R2 y lo traslada a su simétrico, respecto de la recta y = x

Figura 2

T(x, y) = (-x, -y)

Esta transformación toma un punto o figura en R2 y lo traslada a su simétrico respecto del origen (0, 0)

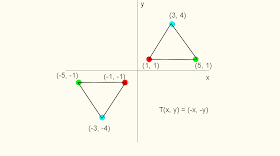
Figura 3

T(x, y) =(nx, ny)

Esta transformación magnifica o reduce un punto o una figura en R2 de acuerdo con la siguiente regla:

Si n >1 magnifica (crece o aumenta)

Si -1

Si n< -1 Magnifica y traslada la figura al cuadrante opuesto por el origen.

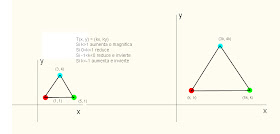
Figura 4

Encontrar una matriz que nos tome el radio vector r de un punto P(x, y) y lo haga rotar un ángulo θ (En sentido antihorario)

Si el ángulo que forma r con la parte positiva del eje x es α, entonces:

x= r cos α (1)

y=r sen α

x’=r cos (α + θ)

y’=r sen (α + θ)

Expandiendo seno y coseno para una suma de ángulos y remplazando de acuerdo con las ecuaciones (1) obtenemos:

x’ = x cos θ – y sen θ

y’= x sen θ +y cos θ

Figura 5

Por tanto, la matriz que nos rota el punto P es:

Comparando con la (2), vemos que el efecto de esta transformación es rotar el vector OP un ángulo antihorario 2θ

Finalmente, qué pasaría si al vector x le aplicáramos la matriz A^o?

A⁰ = A A^-1= I

La respuesta es que nos llevaría el punto P, de nuevo sobre el punto P.

Encontrar una matriz A que nos transforme un punto P en R2 en otro P’ punto en R2, tal que P y P’ sean simétricos respecto de la recta y =√3 x

T:V→W o T:R2→R2 y

T toma un punto en R2 y encuentra su simétrico respecto de la recta: y =√3 x

Sea P(a, b) un punto en V (R2), su simétrico será P’(c, d)

El punto medio de PP’ Está sobre la recta y =√3 x

Las coordenadas de ese punto son:

M ((a + c)/2, (b + d)/2)

Como este punto está sobre la recta y =√3 x

Entonces (b+d)/2 = √3(a +c)/2, que se simplifica a:

d - √3c = a √3 - b (3)

Pero además, la pendiente de PP’ multiplicada por la pendiente de la recta, nos debe dar -1, o sea:

(d –b)/(a – c) = -1/√3

d√3 - b√3 = -a + c

Que simplificamos en

d√3 – c =b√3 – a (4)

Despejando c y d de las ecuaciones (3) y (4) en términos de a y b obtenemos:

c= (-a +√3b)/2

d=(a√3 + b)/2

Cambiando a y b por x e y y c y d por x’ e y’ respectivamente, obtenemos:

x’= (-x +√3y)/2

x’=(x√3 + y)/2

La transformación la podemos expresar así:

T(x, y) = ((-x +√3y)/2, (x√3 + y)/2

Si transformamos la base para R2 (1, 0) y (0, 1) obtenemos:

T (1, 0) = (-1/2, √3/2)

T (0, 1) = (√3/2, 1/2)

La matriz A será

Con lo cual queda demostrado que el punto medio de QQ’ está sobre la recta

y = √3x

Juan Fernando Sanin E

Juanfernando.sanin@gmail.com