Repaso de vectores espaciales con geometía analitica

Medellín, abril de 2022

 

1.   Concepto de vector libre – Base de un espacio en r3 – Base canónica en r3

 

En un principio, los vectores eran magnitudes físicas, cuya descripción no requiere precisar un punto de aplicación, ni siquiera una recta soporte, pues para cualquier punto de aplicación en todo el espacio, sus consecuencias físicas son las mismas. Posteriormente, el concepto se convirtió en una magnitud en abstracto, en la cual sólo importan su dirección, su sentido en esa dirección y su valor absoluto o magnitud.

Un ejemplo lo tenemos en la resultante de todas las fuerzas que actúan sobre un sólido rígido.

El concepto de base es uno de los más importantes en álgebra lineal. Una base es un subconjunto de elementos de nuestro espacio vectorial, con la cual podemos expresar todos los vectores en términos de estos. Primero recordemos que tres vectores u, v y w, son linealmente independientes en el espacio, si uno de ellos no se puede escribir como combinación lineal de los otros dos. Esto implica que, los tres vectores u, v, w, tienen distinta dirección. Además los tres generan todo el espacio, si un vector x cualquiera se puede escribir como combinación lineal de u, v y w, es decit:

 

x = au +bv +cw

 

Los vectores se representaban antes con una letra y una flecha pequeña encima. Con el advenimiento de los computadores y la modernización de la grafía matemática, hoy se representan por una letra en negrilla. Así, a es un número real y a es un vector

La base canónica, que consiste de los siguientes tres vectores:

 

I, j y k, vectores unitarios (de magnitud 1) en la dirección positiva de los ejes x, y z del espacio Cartesiano r3.

 

De esta forma, las coordenadas de un vector cualquiera x son las siguientes

x= ai +bj +ck                        Esta era la la nomenclatura anterior para definir un vector en el espacio ortogonal x, y ,z . No obstante, desde la década de los 90, o tal vez antes, se ha cambiado esta representación, por la tripla x =(a, b, c)           Se sobreentiende, que el primer elemento de la tripla es la magnitud del vector, en sentido de i (dirección positiva del eje x), el segundo es la magnitud en el sentido de j (dirección positiva del eje y) y el tercer elemento es la magnitud del vector en el sentido de k (sentido positivo del eje z)

 

La suma de vectores tiene las siguientes propiedades (en lo que sigue, "u", "v" y "w" son vectores y "t" y "s" son números reales:

• Propiedad asociativa, (u + v) + w = u + (v + w)
• Existencia de elemento neutro, que es el vector nulo (0,0,0),
• Para cada vector u = (x, y, z) existencia de su elemento opuesto –u=(-x,-y,-z)
• Propiedad clausurativa. La suma de vectores en r3, es un vector en r3
• propiedad conmutativa, u + v = v + u

 

2.    Producto escalar de dos vectores.

 

Se define u.v = (magnitud de u) (magnitud de v) cos θ,

Donde θ es el ángulo que forman los dos vectores u y v, cuando se les hace coincidir el origen.

 

El producto escalar no es clausurativo, pues se hace entre dos vectores en r3 y el resultado es un número real.

El producto escalar de dos vectores si es conmutativo        u.v = v.u = (magnitud de u) (magnitud de v) cos θ.

La magnitud de un vector es siempre positiva, equivalente a módulo o valor absoluto de u =/u/ =√ (a1² + b1² + c1²)

Cálculo del producto escalar por componentes.

 u= (a1, b1, c1)

v= (a2, b2, c2)

 

u.v = a1a2 +b1b2 + c1c2 = (magnitud de u) x (magnitud de v) x cos θ      (1)

Notas:

1 si dos vectores son perpendiculares, su producto escalar es igual a 0, porque cos90^o =0

Si un vector u se multiplica escalarmente, por sí mismo, el resultado es la magnitud de u al cuadrado                            u.u = (magnitud de u)x (magnitud de u) x cos 0^o = magnitud de u al cuadrado.

Para demostrar que u.v = /u/ /v/ cos θ = a1a2 + b1b2 +c1c                      (2), nos ayudamos con la ley del coseno de la trigonometría.

│u - v│² = │u│² + │v│² -2│u│ │v│ cos θ         (1 - 1)                 Fig 1

 

u= (a1, b1, c1)                                           │u│ =√ (a1² + b1² +c1²)

v= (a2, b2, c2)                                           │v│ =√ (a2² + b2² +c2²)

 

u – v = (a2-a1, b2-b1, c2-c1)           │u -v│ =√((a1-a2)² + (b1-b2)² + (c1-c2)²)    (3)

Fig 1 Diferencia de vectores y producto escalar de dos vectores.

El procedimiento para demostrar la validez de la ecuación (1), utilizamos la ecuación de la ley del coseno, que se muestra en la figura 1. Resolvemos, por coordenadas, la ecuación (1 -1) y después de hacer la carpintería respectiva, encontraremos que:

a1a2 + b1b2 + c1c2 = │u│.│v│cos θ

 

Ejemplos

1.)

Encontrar el ángulo que forman los vectores A= (1, -1, 3) y B= (2, 1, 0) 

│A│ = √ (1² + (-1)² + 3²) = √11

│B│ = √5

A. B=1x2 +(-1) x1+3x0 = 1 =√11√5 cos θ 

Cos θ =1/√55 = 0.134840            θ = arc cos 0.134840 =82,25 deg 

2) 

Hallar la proyección del vector A = (2, -5,0), sobre el vector B=(5, 1, 0)

A.B = │A││B│ cos θ

La proyección (en magnitud real) de A sobre B es │A│cos θ (no importa el valor de θ

A.B = 10 -5 =5

│A│ cos θ = 5/ │B│ = 5/√26 

Necesitamos es el vector proyección de A sobre B. Ya tenemos la magnitud de ese vector. Necesitamos un vector unitario en la dirección de B.

│B│ = √26

El vector unitario en la dirección de B es B/│B│ = (5, 1, 0)/√26

El vector solicitado es igual a Magnitud x vector unitario = (5/√26) (5, 1, 0)/√26

 

= (5/26) (5, 1, 0)

3)

Encontrar el valor de t, para que los vectores A=(1, 1, -2) y B=(1, 3, t)

Si son perpendiculares A.B =0

 

A.B

 = 1x1+1x3 -2t = 0                 2t=4            t=2           B=(1,3,2) 

1.   Producto vectorial o producto cruz 

El producto vectorial o producto cruz es una operación binaria entre dos vectores, en un espacio tridimensional r3. El resultado es un vector perpendicular a los vectores que se multiplican. 

Si u = (a1, b1, c1) y v= (a2, b2, c2), el producto vectorial uxv es igual a un vector perpendicular a ambos (u y v), definido por el determinante:

 

Como se indicó, la operación producto vectorial es clausurativa, pues el resultado es un vector. Aunque la nomenclatura con i, j y k está en desuso, para el producto vectorial es importante, pues es fácil recordar la definición con el determinante, que antes se mostró.

El vector resultante es perpendicular a cualquier plano, que contenga a u y a v. (todos estos planos son paralelos entre sí) 

Una definición alternativa es que el producto cruz o vectorial de uxv, es un vector perpendicular a los vectores u y v, cuya dirección es perpendicular a ambos y cuyo sentido es el que se encuentra con la regla de la mano derecha, que se muestra en la siguiente figura.

Magnitud de uxv = magnitud de u x magnitud de v x seno del ángulo que forman las 2 direcciones, vistas en sentido positivo.

Figura 2 Regla de la mano derecha para el producto vectorial

4.   Ecuación cartesiana de la recta en el espacio.

 

Consideremos la figura de una recta en el espacio:

Trabajamos en el espacio r3 (x, y, z) y sean i, j, k los vectores unitarios en el sentido de los ejes x, y, z.

Tenemos una recta en el espacio r3. Tenemos un punto conocido Po(xo, yo, zo), que pertenece a la recta, un vector libre v, que tiene la dirección de la recta, (Si lo desplazamos hasta Po, el vector v, estará sobre la recta.

Tenemos un punto P(x, y, z) sobre la recta, que representa cualquier punto de la misma.

Existe el vector PoP que es igual a (x - xo, y - yo, z - zo) y este vector, por estar en la dirección de v, será igual a tv., donde t es un número real.

En la gráfica vemos que el vector OP representa la recta y es igual OP = OPo +tv

Figura 3, ecuación vectorial de una recta en el espacio r3

Si v = (a1, b1, c1) En coordenadas: 

(x, y, z) = (xo, yo, zo) +t (a1, b1, c1)                                     (4)

x=xo +ta1

y=yo + tb1                                                                            (5)

z=zo + tc1 

Las ecuaciones en (5), son muy útiles para encontrar puntos específicos. Se llaman ecuaciones paramétricas de la recta. 

Ejemplos

1) 

Consideremos la ecuación vectorial de la recta que contiene el punto (3, 2, 1) y es paralela al vector (-4, -1, -1)

De acuerdo con las ecuaciones (4) y (5), las ecuaciones vectorial y  paramétricas de esta recta son:

 

(x, y ,z) = (3, 2, 1) + t(–4, –1, –1),  t∈Reales y los vectores a r3 

x=3 -4t

y=2 - t

z=1 - t

Podemos preguntar: ¿Dónde corta esta recta el plano xy? En el plano xy, la z=0

Si z=0 entonces t=1        x= -1, y=1      el punto es (-1, 1, 0)

 ¿Dónde corta esta recta el plano yz? En el plano yz, la x=0

Si x=0 entonces t=3/4       y= 2-3/4= 5/4, z=1-3/4=1/4      el punto es (0, 5/4, 1/4)

 

Cuáles son las coordenadas de un punto P, ubicado sobre la recta, a una distancia de 10 U de Po(3, 2, 1)

PoP = tv

│PoP│ = │tv│ = │t││v│=10

 

│t││v│=10                         │t│= 10/√18

 

Los vectores respuesta son (10/√18) (-4,-1,-1)        y        -(10/√18) (-4,-1,-1)

 

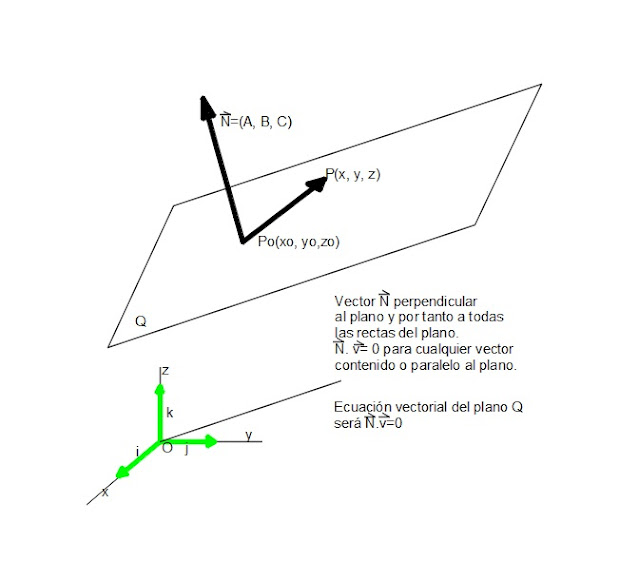
1.    Ecuación vectorial y cartesiana de un plano en r3 

Del plano Q, conocemos el punto Po(xo, yo, zo) sobre el plano y un vector normal N, (es perpendicular a cualquier recta que se encuentre en el plano)

N(A, B, C)    el vector normal al plano, (conocido) 

Si P(x, y, z) es un punto cualquiera del plano, entonces existe el vector que está en el plano PoP = (x – xo, y – yo, z – zo) y producto escalar PoP.N =0                                   (6)

Es la ecuación vectorial del plano Q.

Figura 4 Ecuación vectorial del plano en r3

La ecuación (6) se convierte en (A, B, C). (x – xo, y - yo, z –zo)

 

= A (x – xo) + B (y – yo) +C(z –zo) =0 

Ax+ By +Cz +Axo + Byo Czo=0     Como A, B, C, xo, yo, zo son números reales, entonces la ecuación se transforma en: 

Ax +By +Cz + D = 0 

Para cualquier caso particular, D se obtiene con el punto Po (xo, yo, zo) 

Ejemplo Plano 

1) 

Encontrar la ecuación cartesiana del plano que, pasa por los puntos A(1, 1, 0) ; B(1, 0, 1), C(0, 1, 1)

Necesitamos encontrar el vector normal al plano. Tomamos los vectores AB y AC del plano. El producto vectorial ABxAC nos dará la normal y con esa normal y uno de los puntos, encontramos la ecuación solicitada del plano. 

AB=(0, -1,1)       AC = ( -1, 0, 1) 

Recordemos:

a1=0, b1=-1, c1=1                     a2=-1, b2=0, c2=1

 

N=(-1, -1, -1)         y la ecuación del plano es –x –y –z +D=0

Cualquiera de los tres puntos dados cumple esta ecuación. Con A(1, 1, 0) encontramos D.

-1 -1 +D = 0                D=2

-x –y –z +2 = 0            o simplemente, x +y +z =2 

Preguntemos ahora, ¿Cuál será la intersección de la recta del ejemplo 1, del tema de la recta, con el plano que hemos encontrado?

La recta mencionada es: 

x=3 -4t

y=2 - t

z=1 - t

Simplemente, reemplazamos en la ecuación del plano x + y +z =2, es decir

 

3 - 4t + 2 –t +1 – t = 2; de donde t = 2/3 y llevando este valor a las ecuaciones paramétricas obtenemos 

x = 3 - 8/3 = 1/3

y = 2 - 2/3 = 4/3

z = 1 - 2/3 = 1/3                       El punto (1/3, 4/3, 1/3) satisface ambos, la recta y el plano.

Ángulo que forman dos planos.

El Ángulo formado por dos planos es igual al ángulo agudo determinado por los vectores normales de dichos planos. 

Ejemplo

2)

Encontrar el ángulo que forman los planos q: 2x –y +z=1            s:x+z=-3

 

El vector normal de q es Nq = (2, -1, 1) y el de s: Ns = (1, 0, 1)

El ángulo que forman estos dos planos es:

Nq.Ns =2 + 1 = │Nq││Ns│cosθ           │Nq│=√6          │Ns│=√2

 

cos θ =3/(√6√2) =√3/2 = 0,866025          θ= 30 deg

 

3) Encontrar la ecuación de la recta común, a los planos del ejemplo anterior.

 

Esa recta debe ser perpendicular simultáneamente a los vectores Nq y Ns y además, debemos encontrar un punto de la misma.

El vector en la dirección de la recta es NqxNs

El punto, lo encontramos resolviendo simultáneamente las ecuaciones de q y de s. (infinitas soluciones, pero cualquiera sirve.)

q: 2x –y +z=1            s:x+z=-3     2 ecuaciones con tres incógnitas, tiene infinitas soluciones, todos los puntos de la recta solicitada. Como necesitamos uno le damos un valor arbitrario a z, por ej. z =1, con lo cual concluimos que x = -4

y= 2x+z-1 = -8+1-1=-8         El punto de la recta es P (-4, -8, 1), se chequea en los planos y se ve que pertenece a ambos, luego pertenece a la recta de intersección.

El vector paralelo lo encontramos resolviendo el determinante que hemos venido utilizando para hallar estos productos vectoriales NqxNs = (-1, -1, 1) 

Conocidos el punto (-4, -8, 1) de la recta, que además, hemos comprobado que satisface los dos planos y el vector en la dirección de la recta (-1, -1, 1). Las ecuaciones paramétricas de la recta común serán:

 

x = -4 – t

y = -8 – t

z = 1 + t

Si hacemos t= 0, estamos en el punto (-4, -8, 1). Para encontrar un punto diferente hagamos t=1 y caemos en el punto (-5, -9, 2) y si chequeamos, vemos que satisface los dos planos.

 

 

Juan Fernando Sanín E

juanfernando.sanin@gmail.com