Sea Q(xo,yo) un punto de R2,
no necesariamente en el dominio de f
En una bola abierta con
centro en Q (En este caso una circunferencia, tal como se muestra en la figura
1), tomamos un punto Q1(x,y) en el dominio de f, y en las cercanías de Q(x,y)=(xo+h,yo+k)
Si al acercarnos con el
punto Q1 al punto Q, todo lo que queramos, pero sin llegar a que coincidan, el
valor de f(x,y) siempre es cercano a un valor real L, entonces decimos que:
Lim f(x,y) = L
(x,y)→(xo,yo)
2. Continuidad de la función
Decimos que la función f(x,
y) es continua en el punto Q(xo,yo) si se dan las siguientes tres condiciones:
i)
Lim f(x,y) Existe
(x,y)→(xo,yo)
ii)
f(xo,yo) = L
iii)
Lim f(x,y) = f(xo,yo) = L
(x,y)→(xo,yo)
Ejemplos
1.Calcular lim (x+2y)
(x,y)→(1,2)
Basta reemplazar la x por 1
y la y por 2 y el resultado del límite es
lim (x+2y)=5
(x,y)→(1,2)
2.Calcular lim (cosx+1/y)
cuando (x,y) → (0,0)
Al reemplazar encontramos
lo siguiente cos0 + 1/0
Como 1/y cuando y→0 no existe,
entonces el límite no existe.
En el ejemplo 1 se concluye
además, que la función es continua en (1,2)
Mientras que en el ejemplo
2 se concluye que la función es discontinua en (0,0)
3. Límite
de la función escalar z=f(x1, x2,……….xn)
Se trata de una función de
Rn en R, en la cual, a cada vector x=(x1, x2,…,xn) le corresponde un valor único z real en R.
Aquí ya no es posible hacer
un gráfico del problema.
Tomemos un punto
Q(xo1,xo2,….,xon), no necesariamente en el dominio de f, este punto es el
vector xo
Ahora tomamos otro punto
Q1, este si en el dominio de f y en las cercanías de Q.
x=(x1,x2,…..,xn)
= (xo1+h1, xo2+h2,…..,xon+hn)
Ahora bien, acercamos el
vector x al vector xo, lo cual se logra haciendo que las
componentes del vector h = (h1, h2,
….,hn) se hagan tan pequeñas como queramos, pero no 0.
Es decir, arrimamos el
punto Q1 hasta el punto Q todo lo que queramos, pero sin hacerlos coincidir.
Si al hacer esto, el valor
de la función f(x1,x2,….,xn) toma valores cercanos a L y más cercanos mientras
mas acerquemos Q1 a Q, decimos de manera intuitiva que:
Lim f(x1. x2, …,xn) = L
x→xo
4. Continuidad dela función escalar
Para que una función
f(x1,x2, …..,xn) sea continua en punto (xo1,xo2, ,xon) se requiere que se cumplan tres
condiciones:
i)lim f(x1,x2,….,xn) Existe
x→xo
ii)f(xo1, xo2,….,xon) = L
iii)lim f(x1,x2,….,xn)
=f(xo1, xo2,….,xon)
x→xo
Ejemplo
Calcular el límite de la
función f(x, y, z) =x2+y+cosz, cuando (x, y, z) →(1, 2, 0)
Basta reemplazar
Lim x2+y+cosz =
12+2+cos0=4
(x, y, z) →(1, 2, 0)
En este caso también
podemos concluir que la función es continua en (1, 2, 0)
5. Funciones
vectoriales
Una función vectorial
generalizada es una función que toma un vector x en Rn y lo convierte en otro vector f(x) en en Rm
f:Rn→Rm
x→f(x)
x=(x1,
x2,….,xn)
f(x) = (f1(x), f2(x), , fm(x))
La función vectorial f es un vector cuyas componentes son
(f1, f2,….,fm)
Para que la función
vectorial f sea continua es
necesario que todas sus funciones componentes lo sean.
Igualmente, si el dominio
de f1 es D1, el de f2 es D2, y el de fm es Dm
El dominio de la función
vectorial f será la intersección de todos los dominios D1ПD2П……..ПDm
Para que la función
vectorial sea derivable en un vector xo, es necesario que todas las funciones f1, f2,…fm lo sean
y tengan todas las derivadas parciales posibles.
Construyamos una matrix en
la que las filas correspondan a las funciones fi y las columnas a las
componentes xi del vector
Ejemplo
Calcular el límite de la siguiente función
vectorial:
Lim (sen(πt/2) /t,( t2-1)/(1-t),
e-1/abs(t-1))
t→1
Lim (sen(πt/2)
/t,-(t+1)(t-1)/(t-1), e-1/abs(t-1))
t→1
=(1, -2, 0)
Ejemplo
Calcular el límite de la
siguiente función vectorial:
Lim (xarctang xy, ln x/y,
(x2-2xy+y2)/(x2y-y2))
r→ro
ro=(1, 1)
Lim (xarctang xy, ln x/y,
(x2-2xy+y2)/(x2y-y3))
r→ro
Lim (xarctang xy, ln x/y,
(x-y)2/(y(x+y)(x-y))
r→ro
Reemplazando obtenemos
=(π/4, 0, 0)
Ejemplo
Dada la siguiente
función vectorial
F(x,y,z) =( exyz,
xyln(xyz), tan-1x2y2z2)
Encontrar la matriz
Jacobiana.
En ro=(1,1,1), encontrar el incremento
df si dr=(0,01,0,01,0,01)
Para encontrar la
matriz Jacobiana debemos encontrar una matriz en que las filas son las
derivadas parciales de f1, f2 y f3 respecto de x, y y z.
Ejemplo
V(xy,
yz, xz) es una función vectorial que representa el flujo de un líquido.
│v│ en m/seg
Calcular la rapidez de
crecimiento del flujo en el punto (4,2,2)
En la dirección de un
vector espacial que forma un ángulo de 60o con el eje x y 45o con
el eje y.
Primero encontremos el
vector anterior.
u=(u1,
u2, u3) unitario, forma un ángulo de 60º con el eje x y de 45º con el eje y.
u.i
=│u│.
│i│. cos 60o = u1 Siendo u e i unitarios, la
componente u1= ½
u.j
= │u│ │ j│. cos 45º = u2 , por tanto
u2=√2/2
ui2+u22+u32
= 1 Por tanto u3= ½
El vector u unitario para la derivada direccional
es u = (1/2, √2/2, 1/2)
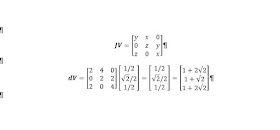
El próximo paso es
encontrar la matriz Jacoviana de V